12 Sum and Difference Identities
Learning Objectives
In this section, you will:
- Use sum and difference formulas for cosine.
- Use sum and difference formulas for sine.
- Use sum and difference formulas for tangent.
- Use sum and difference formulas for cofunctions.
- Use sum and difference formulas to verify identities.

How can the height of a mountain be measured? What about the distance from Earth to the sun? Like many seemingly impossible problems, we rely on mathematical formulas to find the answers. The trigonometric identities, commonly used in mathematical proofs, have had real-world applications for centuries, including their use in calculating long distances.
The trigonometric identities we will examine in this section can be traced to a Persian astronomer who lived around 950 AD, but the ancient Greeks discovered these same formulas much earlier and stated them in terms of chords. These are special equations or postulates, true for all values input to the equations, and with innumerable applications.
In this section, we will learn techniques that will enable us to solve problems such as the ones presented above. The formulas that follow will simplify many trigonometric expressions and equations. Keep in mind that, throughout this section, the term formula is used synonymously with the word identity.
Using the Sum and Difference Formulas for Cosine
Finding the exact value of the sine, cosine, or tangent of an angle is often easier if we can rewrite the given angle in terms of two angles that have known trigonometric values. We can use the special angles, which we can review in the unit circle shown in (Figure 2).
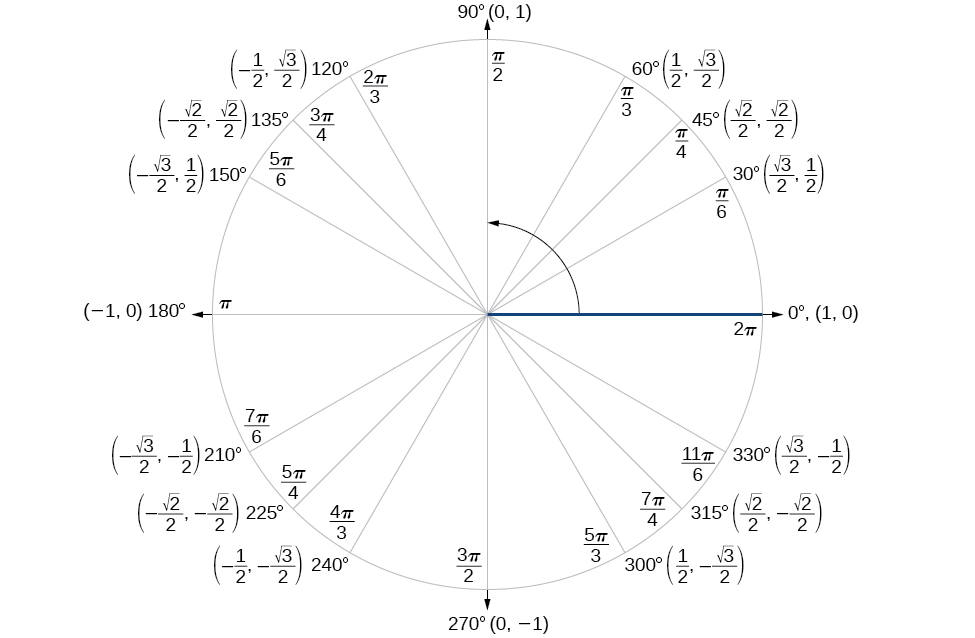
We will begin with the sum and difference formulas for cosine, so that we can find the cosine of a given angle if we can break it up into the sum or difference of two of the special angles. See (Figure).
| Sum formula for cosine | |
| Difference formula for cosine |
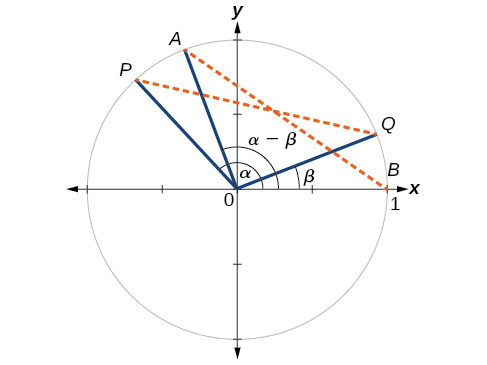
First, we will prove the difference formula for cosines. Let’s consider two points on the unit circle. See (Figure). Point![]() is at an angle
is at an angle![]() from the positive x-axis with coordinates
from the positive x-axis with coordinates![]() and point
and point![]() is at an angle of
is at an angle of![]() from the positive x-axis with coordinates
from the positive x-axis with coordinates![]() Note the measure of angle
Note the measure of angle![]() is
is![]()
Label two more points:![]() at an angle of
at an angle of![]() from the positive x-axis with coordinates
from the positive x-axis with coordinates![]() and point
and point![]() with coordinates
with coordinates![]() Triangle
Triangle![]() is a rotation of triangle
is a rotation of triangle![]() and thus the distance from
and thus the distance from![]() to
to![]() is the same as the distance from
is the same as the distance from![]() to
to![]()
We can find the distance from![]() to
to![]() using the distance formula.
using the distance formula.
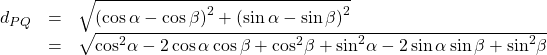
Then we apply the Pythagorean identity and simplify.
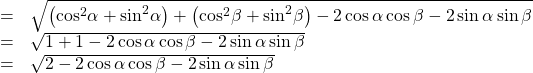
Similarly, using the distance formula we can find the distance from![]() to
to![]()
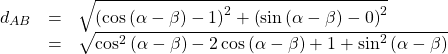
Applying the Pythagorean identity and simplifying we get:
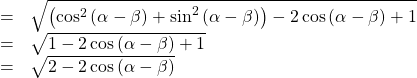
Because the two distances are the same, we set them equal to each other and simplify.
Finally we subtract![]() from both sides and divide both sides by
from both sides and divide both sides by![]()
Thus, we have the difference formula for cosine. We can use similar methods to derive the cosine of the sum of two angles.
Sum and Difference Formulas for Cosine
These formulas can be used to calculate the cosine of sums and differences of angles.
How To
Given two angles, find the cosine of the difference between the angles.
- Write the difference formula for cosine.
- Substitute the values of the given angles into the formula.
- Simplify.
Finding the Exact Value Using the Formula for the Cosine of the Difference of Two Angles
Using the formula for the cosine of the difference of two angles, find the exact value of![]()
Show Solution
Begin by writing the formula for the cosine of the difference of two angles. Then substitute the given values.
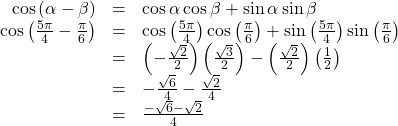
Keep in mind that we can always check the answer using a graphing calculator in radian mode.
Try It
Find the exact value of![]() Hint:
Hint: ![]()
Show Solution
![]()
Finding the Exact Value Using the Formula for the Sum of Two Angles for Cosine
Find the exact value of![]()
Show Solution
As ![]() we can evaluate
we can evaluate ![]() as
as ![]()
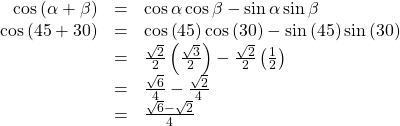
Keep in mind that we can always check the answer using a graphing calculator in degree mode.
Analysis
Note that we could have also solved this problem using the fact that![]()
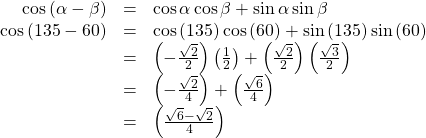
Try It
Find the exact value of![]()
Show Solution
![]()
Using the Sum and Difference Formulas for Sine
The sum and difference formulas for sine can be derived in the same manner as those for cosine, and they resemble the cosine formulas.
Sum and Difference Formulas for Sine
These formulas can be used to calculate the sines of sums and differences of angles.
How To
Given two angles, find the sine of the difference between the angles.
- Write the difference formula for sine.
- Substitute the given angles into the formula.
- Simplify.
Using Sum and Difference Identities to Evaluate the Difference of Angles
To find ![]() , we can use the sum and difference identities to evaluate the difference of the angles. Note that we can find it in two ways, with the same results.
, we can use the sum and difference identities to evaluate the difference of the angles. Note that we can find it in two ways, with the same results.
Show Solution
- Let’s begin by writing the formula and substitute the given angles.
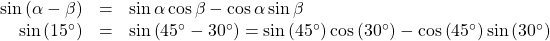
Next, we need to find the values of the trigonometric expressions.
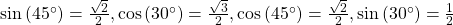
Now we can substitute these values into the equation and simplify.
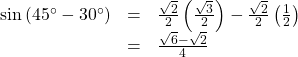
- Again, we write the formula and substitute the given angles.
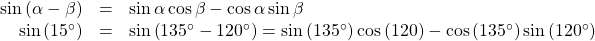
Next, we find the values of the trigonometric expressions.
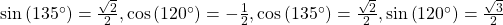
Now we can substitute these values into the equation and simplify.
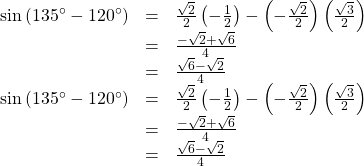
Finding the Exact Value of an Expression Involving an Inverse Trigonometric Function
Find the exact value of ![]() Then check the answer with a graphing calculator.
Then check the answer with a graphing calculator.
Show Solution
The pattern displayed in this problem is ![]() Let
Let ![]() and
and ![]() Then we can write
Then we can write
We will use the Pythagorean identities to find ![]() and
and ![]()
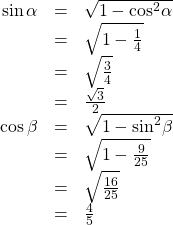
Using the sum formula for sine,
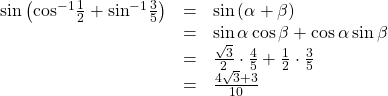
Using the Sum and Difference Formulas for Tangent
Finding exact values for the tangent of the sum or difference of two angles is a little more complicated, but again, it is a matter of recognizing the pattern.
Finding the sum of two angles formula for tangent involves taking quotient of the sum formulas for sine and cosine and simplifying. Recall,![]()
Let’s derive the sum formula for tangent.

We can derive the difference formula for tangent in a similar way.
Sum and Difference Formulas for Tangent
The sum and difference formulas for tangent are:
How To
Given two angles, find the tangent of the sum of the angles.
- Write the sum formula for tangent.
- Substitute the given angles into the formula.
- Simplify.
Finding the Exact Value of an Expression Involving Tangent
Find the exact value of ![]()
Show Solution
Let’s first write the sum formula for tangent and then substitute the given angles into the formula.
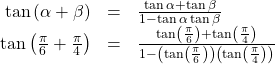
Next, we determine the individual function values within the formula:
So we have
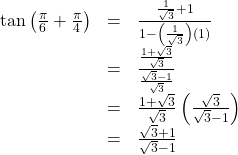
Try It
Find the exact value of ![]() . Note that
. Note that ![]()
Show Solution
![]()
Finding Multiple Sums and Differences of Angles
Given ![]() find
find
Show Solution
We can use the sum and difference formulas to identify the sum or difference of angles when the ratio of sine, cosine, or tangent is provided for each of the individual angles. To do so, we construct what is called a reference triangle to help find each component of the sum and difference formulas.
- To find
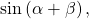 we begin with
we begin with 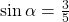 and
and 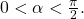 The side opposite
The side opposite 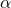 has length 3, the hypotenuse has length 5, and
has length 3, the hypotenuse has length 5, and 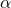 is in the first quadrant. See (Figure 4). Using the Pythagorean Theorem, we can find the length of side
is in the first quadrant. See (Figure 4). Using the Pythagorean Theorem, we can find the length of side 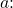
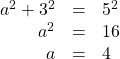

Figure 4. Since
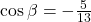 and
and 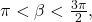 the side adjacent to
the side adjacent to 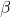 is
is 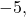 the hypotenuse is 13, and
the hypotenuse is 13, and 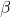 is in the third quadrant. See (Figure 5 ). Again, using the Pythagorean Theorem, we have
is in the third quadrant. See (Figure 5 ). Again, using the Pythagorean Theorem, we have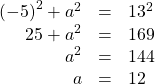
Since
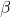 is in the third quadrant,
is in the third quadrant, 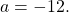

Figure 5. The next step is finding the cosine of
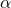 and the sine of
and the sine of 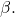 The cosine of
The cosine of 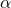 is the adjacent side over the hypotenuse. We can find it from the triangle in (Figure):
is the adjacent side over the hypotenuse. We can find it from the triangle in (Figure): 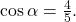 We can also find the sine of
We can also find the sine of 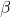 from the triangle in (Figure), as opposite side over the hypotenuse:
from the triangle in (Figure), as opposite side over the hypotenuse: 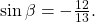 Now we are ready to evaluate
Now we are ready to evaluate 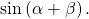
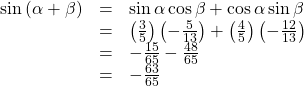
- We can find
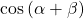 in a similar manner. We substitute the values according to the formula.
in a similar manner. We substitute the values according to the formula.
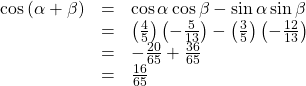
- For
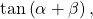 if
if 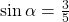 and
and 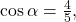 then
then
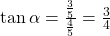
If
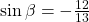 and
and 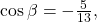
then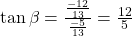
Then,
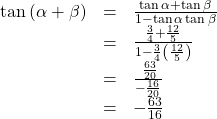
- To find
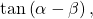 we have the values we need. We can substitute them in and evaluate.
we have the values we need. We can substitute them in and evaluate.
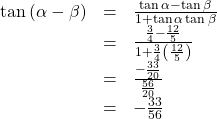
Analysis
A common mistake when addressing problems such as this one is that we may be tempted to think that ![]() and
and ![]() are angles in the same triangle, which of course, they are not. Also note that
are angles in the same triangle, which of course, they are not. Also note that
Using Sum and Difference Formulas for Cofunctions
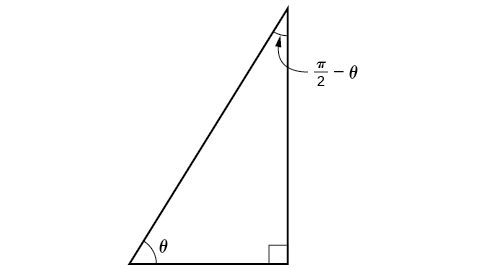
Now that we can find the sine, cosine, and tangent functions for the sums and differences of angles, we can use them to do the same for their cofunctions. You may recall from Right Triangle Trigonometry that, if the sum of two positive angles is ![]() those two angles are complements, and the sum of the two acute angles in a right triangle is
those two angles are complements, and the sum of the two acute angles in a right triangle is ![]() so they are also complements. In (Figure 6), notice that if one of the acute angles is labeled as
so they are also complements. In (Figure 6), notice that if one of the acute angles is labeled as ![]() then the other acute angle must be labeled
then the other acute angle must be labeled ![]()
Notice also that ![]() which is opposite over hypotenuse. Thus, when two angles are complementary, we can say that the sine of
which is opposite over hypotenuse. Thus, when two angles are complementary, we can say that the sine of ![]() equals the cofunction of the complement of
equals the cofunction of the complement of ![]() Similarly, tangent and cotangent are cofunctions, and secant and cosecant are cofunctions.
Similarly, tangent and cotangent are cofunctions, and secant and cosecant are cofunctions.
From these relationships, the cofunction identities are formed. Recall that you first encountered these identities in The Unit Circle: Sine and Cosine Functions.
Notice that the formulas in the table may also justified algebraically using the sum and difference formulas. For example, using
we can write
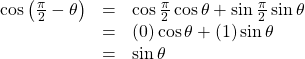
Finding a Cofunction with the Same Value as the Given Expression
Write ![]() in terms of its cofunction.
in terms of its cofunction.
Show Solution
The cofunction of ![]() Thus,
Thus,
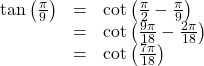
Try It
Write ![]() in terms of its cofunction.
in terms of its cofunction.
Show Solution
![]()
Using the Sum and Difference Formulas to Verify Identities
Verifying an identity means demonstrating that the equation holds for all values of the variable. It helps to be very familiar with the identities or to have a list of them accessible while working the problems. Reviewing the general rules presented earlier may help simplify the process of verifying an identity.
How To
Given an identity, verify using sum and difference formulas.
- Begin with the expression on the side of the equal sign that appears most complex. Rewrite that expression until it matches the other side of the equal sign. Occasionally, we might have to alter both sides, but working on only one side is the most efficient.
- Look for opportunities to use the sum and difference formulas.
- Rewrite sums or differences of quotients as single quotients.
- If the process becomes cumbersome, rewrite the expression in terms of sines and cosines.
Verifying an Identity Involving Sine
Verify the identity ![]()
Show Solution
We see that the left side of the equation includes the sines of the sum and the difference of angles.
We can rewrite each using the sum and difference formulas.
We see that the identity is verified.
Verifying an Identity Involving Tangent
Verify the following identity.
Show Solution
We can begin by rewriting the numerator on the left side of the equation.
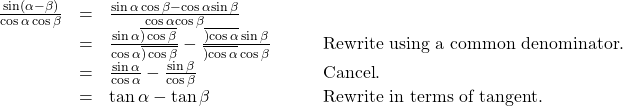
We see that the identity is verified. In many cases, verifying tangent identities can successfully be accomplished by writing the tangent in terms of sine and cosine.
Try It
Verify the identity: ![]()
Show Solution
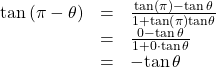
Using Sum and Difference Formulas to Solve an Application Problem
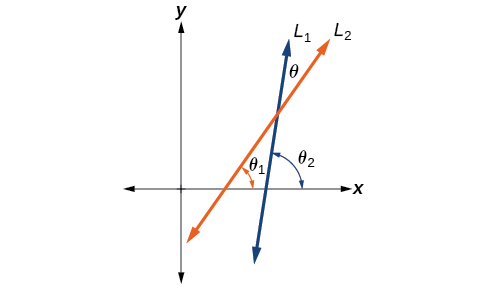
Let ![]() and
and ![]() denote two non-vertical intersecting lines, and let
denote two non-vertical intersecting lines, and let ![]() denote the acute angle between
denote the acute angle between ![]() and
and ![]() See (Figure 7). Show that
See (Figure 7). Show that
where ![]() and
and ![]() are the slopes of
are the slopes of ![]() and
and ![]() respectively. (Hint: Use the fact that
respectively. (Hint: Use the fact that ![]() and
and ![]() )
)
Show Solution
Using the difference formula for tangent, this problem does not seem as daunting as it might.
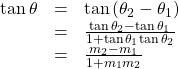
Investigating a Guy-wire Problem
For a climbing wall, a guy-wire![]() is attached 47 feet high on a vertical pole. Added support is provided by another guy-wire
is attached 47 feet high on a vertical pole. Added support is provided by another guy-wire![]() attached 40 feet above ground on the same pole. If the wires are attached to the ground 50 feet from the pole, find the angle
attached 40 feet above ground on the same pole. If the wires are attached to the ground 50 feet from the pole, find the angle![]() between the wires. See (Figure 8).
between the wires. See (Figure 8).
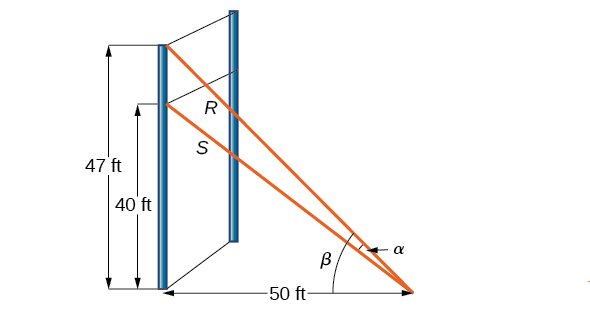
Show Solution
Let’s first summarize the information we can gather from the diagram. As only the sides adjacent to the right angle are known, we can use the tangent function. Notice that ![]() and
and ![]() We can then use difference formula for tangent.
We can then use difference formula for tangent.
Now, substituting the values we know into the formula, we have
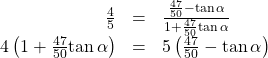
Use the distributive property, and then simplify the functions.
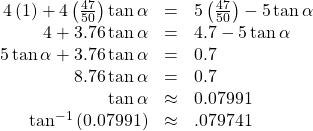
Now we can calculate the angle in degrees.
Analysis
Occasionally, when an application appears that includes a right triangle, we may think that solving is a matter of applying the Pythagorean Theorem. That may be partially true, but it depends on what the problem is asking and what information is given.
Access these online resources for additional instruction and practice with sum and difference identities.
Key Equations
| Sum Formula for Cosine | |
| Difference Formula for Cosine | |
| Sum Formula for Sine | |
| Difference Formula for Sine | |
| Sum Formula for Tangent | |
| Difference Formula for Tangent | |
| Cofunction identities | 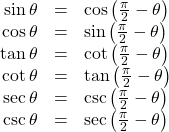 |
Key Concepts
- The sum formula for cosines states that the cosine of the sum of two angles equals the product of the cosines of the angles minus the product of the sines of the angles. The difference formula for cosines states that the cosine of the difference of two angles equals the product of the cosines of the angles plus the product of the sines of the angles.
- The sum and difference formulas can be used to find the exact values of the sine, cosine, or tangent of an angle. See (Figure) and (Figure).
- The sum formula for sines states that the sine of the sum of two angles equals the product of the sine of the first angle and cosine of the second angle plus the product of the cosine of the first angle and the sine of the second angle. The difference formula for sines states that the sine of the difference of two angles equals the product of the sine of the first angle and cosine of the second angle minus the product of the cosine of the first angle and the sine of the second angle. See (Figure).
- The sum and difference formulas for sine and cosine can also be used for inverse trigonometric functions. See (Figure).
- The sum formula for tangent states that the tangent of the sum of two angles equals the sum of the tangents of the angles divided by 1 minus the product of the tangents of the angles. The difference formula for tangent states that the tangent of the difference of two angles equals the difference of the tangents of the angles divided by 1 plus the product of the tangents of the angles. See (Figure).
- The Pythagorean Theorem along with the sum and difference formulas can be used to find multiple sums and differences of angles. See (Figure).
- The cofunction identities apply to complementary angles and pairs of reciprocal functions. See (Figure).
- Sum and difference formulas are useful in verifying identities. See (Figure) and (Figure).
- Application problems are often easier to solve by using sum and difference formulas. See (Figure) and (Figure).
Section Exercises
Verbal
Explain the basis for the cofunction identities and when they apply.
Show Solution
The cofunction identities apply to complementary angles. Viewing the two acute angles of a right triangle, if one of those angles measures ![]() the second angle measures
the second angle measures ![]() Then
Then ![]() The same holds for the other cofunction identities. The key is that the angles are complementary.
The same holds for the other cofunction identities. The key is that the angles are complementary.
Is there only one way to evaluate ![]() Explain how to set up the solution in two different ways, and then compute to make sure they give the same answer.
Explain how to set up the solution in two different ways, and then compute to make sure they give the same answer.
Explain to someone who has forgotten the even-odd properties of sinusoidal functions how the addition and subtraction formulas can determine this characteristic for ![]() and
and ![]() (Hint:
(Hint:![]() )
)
Show Solution
![]() so
so ![]() is odd.
is odd.![]() so
so![]() is even.
is even.
Algebraic
For the following exercises, find the exact value.
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
For the following exercises, rewrite in terms of![]() and
and![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
For the following exercises, simplify the given expression.
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
For the following exercises, find the requested information.
Given that ![]() and
and ![]() with
with ![]() and
and ![]() both in the interval
both in the interval![]() find
find ![]() and
and ![]()
Given that ![]() and
and ![]() with
with ![]() and
and ![]() both in the interval
both in the interval![]() find
find ![]() and
and![]()
Show Solution
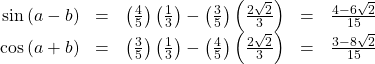
For the following exercises, find the exact value of each expression.
![]()
![]()
Show Solution
![]()
![]()
Graphical
For the following exercises, simplify the expression, and then graph both expressions as functions to verify the graphs are identical. Confirm your answer using a graphing calculator.
![]()
Show Solution
![]()

![]()
![]()
Show Solution
![]()

![]()
![]()
Show Solution
![]()

![]()
![]()
Show Solution
![]()

![]()
For the following exercises, use a graph to determine whether the functions are the same or different. If they are the same, show why. If they are different, replace the second function with one that is identical to the first. (Hint: think, 2x=x+x.
)
![]()
Show Solution
They are the same.
![]()
![]()
Show Solution
They are the different, try![]()
![]()
![]()
Show Solution
They are the same.
![]()
![]()
Show Solution
They are the different, try ![]()
![]()
![]()
Show Solution
They are different, try ![]()
Technology
For the following exercises, find the exact value algebraically, and then confirm the answer with a calculator to the fourth decimal point.
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]() or 0.9659
or 0.9659
![]()
Extensions
For the following exercises, prove the identities provided.
![]()
Show Solution
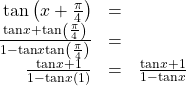
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
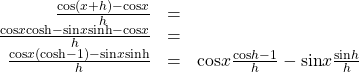
For the following exercises, prove or disprove the statements.
![]()
![]()
Show Solution
True
![]()
If![]() and
and![]() are angles in the same triangle, then prove or disprove
are angles in the same triangle, then prove or disprove![]()
Show Solution
True. Note that ![]() and expand the right hand side.
and expand the right hand side.
If![]() and
and![]() are angles in the same triangle, then prove or disprove
are angles in the same triangle, then prove or disprove![]()
