14 Solving Trigonometric Equations
Learning Objectives
In this section, you will:
- Solve linear trigonometric equations in sine and cosine.
- Solve equations involving a single trigonometric function.
- Solve trigonometric equations using a calculator.
- Solve trigonometric equations that are quadratic in form.
- Solve trigonometric equations using fundamental identities.
- Solve trigonometric equations with multiple angles.
- Solve right triangle problems.

Thales of Miletus (circa 625–547 BC) is known as the founder of geometry. The legend is that he calculated the height of the Great Pyramid of Giza in Egypt using the theory of similar triangles, which he developed by measuring the shadow of his staff. Based on proportions, this theory has applications in a number of areas, including fractal geometry, engineering, and architecture. Often, the angle of elevation and the angle of depression are found using similar triangles.
In earlier sections of this chapter, we looked at trigonometric identities. Identities are true for all values in the domain of the variable. In this section, we begin our study of trigonometric equations to study real-world scenarios such as the finding the dimensions of the pyramids.
Solving Linear Trigonometric Equations in Sine and Cosine
Trigonometric equations are, as the name implies, equations that involve trigonometric functions. Similar in many ways to solving polynomial equations or rational equations, only specific values of the variable will be solutions, if there are solutions at all. Often we will solve a trigonometric equation over a specified interval. However, just as often, we will be asked to find all possible solutions, and as trigonometric functions are periodic, solutions are repeated within each period. In other words, trigonometric equations may have an infinite number of solutions. Additionally, like rational equations, the domain of the function must be considered before we assume that any solution is valid. The period of both the sine function and the cosine function is ![]() In other words, every
In other words, every ![]() units, the y-values repeat. If we need to find all possible solutions, then we must add
units, the y-values repeat. If we need to find all possible solutions, then we must add ![]() where
where ![]() is an integer, to the initial solution. Recall the rule that gives the format for stating all possible solutions for a function where the period is
is an integer, to the initial solution. Recall the rule that gives the format for stating all possible solutions for a function where the period is ![]()
There are similar rules for indicating all possible solutions for the other trigonometric functions. Solving trigonometric equations requires the same techniques as solving algebraic equations. We read the equation from left to right, horizontally, like a sentence. We look for known patterns, factor, find common denominators, and substitute certain expressions with a variable to make solving a more straightforward process. However, with trigonometric equations, we also have the advantage of using the identities we developed in the previous sections.
Solving a Linear Trigonometric Equation Involving the Cosine Function
Find all possible exact solutions for the equation![]()
Show Solution
From the unit circle, we know that
These are the solutions in the interval ![]() All possible solutions are given by
All possible solutions are given by
where![]() is an integer.
is an integer.
Solving a Linear Equation Involving the Sine Function
Find all possible exact solutions for the equation![]()
Show Solution
Solving for all possible values of t means that solutions include angles beyond the period of ![]() From (Figure), we can see that the solutions are
From (Figure), we can see that the solutions are ![]() and
and ![]() But the problem is asking for all possible values that solve the equation. Therefore, the answer is
But the problem is asking for all possible values that solve the equation. Therefore, the answer is
where![]() is an integer.
is an integer.
How To
Given a trigonometric equation, solve using algebra.
- Look for a pattern that suggests an algebraic property, such as the difference of squares or a factoring opportunity.
- Substitute the trigonometric expression with a single variable, such as
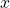 or
or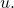
- Solve the equation the same way an algebraic equation would be solved.
- Substitute the trigonometric expression back in for the variable in the resulting expressions.
- Solve for the angle.
Solve the Linear Trigonometric Equation
Solve the equation exactly: ![]()
Show Solution
Use algebraic techniques to solve the equation.
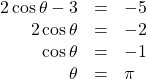
Try It
Solve exactly the following linear equation on the interval![]()
Show Solution
![]()
Solving Equations Involving a Single Trigonometric Function
When we are given equations that involve only one of the six trigonometric functions, their solutions involve using algebraic techniques and the unit circle (see (Figure)). We need to make several considerations when the equation involves trigonometric functions other than sine and cosine. Problems involving the reciprocals of the primary trigonometric functions need to be viewed from an algebraic perspective. In other words, we will write the reciprocal function, and solve for the angles using the function. Also, an equation involving the tangent function is slightly different from one containing a sine or cosine function. First, as we know, the period of tangent is![]() not
not![]() Further, the domain of tangent is all real numbers with the exception of odd integer multiples of
Further, the domain of tangent is all real numbers with the exception of odd integer multiples of![]() unless, of course, a problem places its own restrictions on the domain.
unless, of course, a problem places its own restrictions on the domain.
Solving a Problem Involving a Single Trigonometric Function
Solve the problem exactly: ![]()
Show Solution
As this problem is not easily factored, we will solve using the square root property. First, we use algebra to isolate![]() Then we will find the angles.
Then we will find the angles.
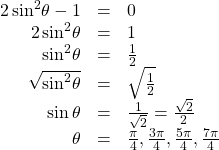
Solving a Trigonometric Equation Involving Cosecant
Solve the following equation exactly: ![]()
Show Solution
We want all values of ![]() for which
for which ![]() over the interval
over the interval ![]()
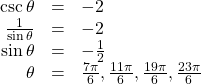
Analysis
As ![]() notice that all four solutions are in the third and fourth quadrants.
notice that all four solutions are in the third and fourth quadrants.
Solving an Equation Involving Tangent
Find all possible exact solutions for the equation exactly:![]()
Show Solution
Recall that the tangent function has a period of![]() On the interval
On the interval![]() and at the angle of
and at the angle of![]() the tangent has a value of 1. However, the angle we want is
the tangent has a value of 1. However, the angle we want is![]() Thus, if
Thus, if![]() then
then
Over the interval ![]() we have two solutions:
we have two solutions:
Try It
Find all exact solutions for![]()
Show Solution
![]()
Identify all Solutions to the Equation Involving Tangent
Identify all exact solutions to the equation![]()
Show Solution
We can solve this equation using only algebra. Isolate the expression![]() on the left side of the equals sign.
on the left side of the equals sign.
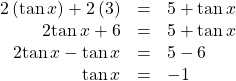
There are two angles on the unit circle that have a tangent value of ![]() and
and ![]()
Solve Trigonometric Equations Using a Calculator
Not all functions can be solved exactly using only the unit circle. When we must solve an equation involving an angle other than one of the special angles, we will need to use a calculator. Make sure it is set to the proper mode, either degrees or radians, depending on the criteria of the given problem. If the mode is not explicitly stated, it may be implied by other criteria, such as the given interval.
Using a Calculator to Solve a Trigonometric Equation Involving Sine
Use a calculator to solve the equation![]() where
where![]() is in radians.
is in radians.
Show Solution
Make sure mode is set to radians. To find ![]() use the inverse sine function. On most calculators, you will need to push the 2ND button and then the SIN button to bring up the
use the inverse sine function. On most calculators, you will need to push the 2ND button and then the SIN button to bring up the![]() function. What is shown on the screen is
function. What is shown on the screen is ![]() The calculator is ready for the input within the parentheses. For this problem, we enter
The calculator is ready for the input within the parentheses. For this problem, we enter ![]() and press ENTER. Thus, to four decimals places,
and press ENTER. Thus, to four decimals places,
The solution is
Analysis
Note that a calculator will only return an angle in quadrants I or IV for the sine function, since that is the range of the inverse sine. The other angle is obtained by using ![]()
Using a Calculator to Solve a Trigonometric Equation Involving Secant
Use a calculator to solve the equation ![]() giving your answer in radians.
giving your answer in radians.
Show Solution
We can begin with some algebra.
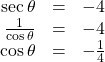
Check that the MODE is in radians. Now use the inverse cosine function.
Since ![]() and
and ![]() 1.8235 is between these two numbers, thus
1.8235 is between these two numbers, thus ![]() is in quadrant II. Cosine is also negative in quadrant III. Note that a calculator will only return an angle in quadrants I or II for the cosine function, since that is the range of the inverse cosine. See (Figure 2).
is in quadrant II. Cosine is also negative in quadrant III. Note that a calculator will only return an angle in quadrants I or II for the cosine function, since that is the range of the inverse cosine. See (Figure 2).

So, we also need to find the measure of the angle in quadrant III. In quadrant III, the reference angle is![]() The other solution in quadrant III is
The other solution in quadrant III is![]()
The solutions are ![]() and
and ![]()
Try It
Using a calculator, solve ![]()
Show Solution
![]() and
and ![]()
Solving Trigonometric Equations in Quadratic Form
Solving a quadratic equation may be more complicated, but once again, we can use algebra as we would for any quadratic equation. Look at the pattern of the equation. Is there more than one trigonometric function in the equation, or is there only one? Which trigonometric function is squared? If there is only one function represented and one of the terms is squared, think about the standard form of a quadratic. Replace the trigonometric function with a variable such as![]() or
or![]() If substitution makes the equation look like a quadratic equation, then we can use the same methods for solving quadratics to solve the trigonometric equations.
If substitution makes the equation look like a quadratic equation, then we can use the same methods for solving quadratics to solve the trigonometric equations.
Solving a Trigonometric Equation in Quadratic Form
Solve the equation exactly: ![]()
Show Solution
We begin by using substitution and replacing cos ![]() with
with ![]() It is not necessary to use substitution, but it may make the problem easier to solve visually. Let
It is not necessary to use substitution, but it may make the problem easier to solve visually. Let ![]() We have
We have
The equation cannot be factored, so we will use the quadratic formula![]()
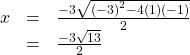
Replace ![]() with
with ![]() and solve.
and solve.
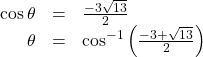
Note that only the + sign is used. The possible solutions with a – sign falls outside the domain of the cosine function, [-1,1]. We can verify this with a calculator to find the approximate value ![]() . To determine a second solution in the interval, use the first solution:
. To determine a second solution in the interval, use the first solution:
This terminal side of the angle lies in quadrant I. Since cosine is also positive in quadrant IV, the second solution is
Solving a Trigonometric Equation in Quadratic Form by Factoring
Solve the equation exactly: ![]()
Show Solution
Using grouping, this quadratic can be factored. Either make the real substitution, ![]() or imagine it, as we factor:
or imagine it, as we factor:
Now set each factor equal to zero.
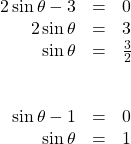
Next solve for ![]() as the range of the sine function is
as the range of the sine function is ![]() However,
However, ![]() giving the solution
giving the solution ![]()
Analysis
Make sure to check all solutions on the given domain as some factors have no solution.
Try It
Solve ![]() [Hint: Make a substitution to express the equation only in terms of cosine.]
[Hint: Make a substitution to express the equation only in terms of cosine.]
Show Solution
![]()
Solving a Trigonometric Equation Using Algebra
Solve exactly:
Show Solution
This problem should appear familiar as it is similar to a quadratic. Using substitution, let ![]() The equation becomes
The equation becomes![]() We begin by factoring:
We begin by factoring:
Set each factor equal to zero.
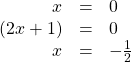
Then, substitute ![]() for
for ![]() back into the equation the original expression. Thus,
back into the equation the original expression. Thus,
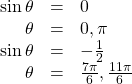
The solutions within the domain ![]() are
are ![]()
If we prefer not to substitute, we can solve the equation by following the same pattern of factoring as in example 11 and setting each factor equal to zero.
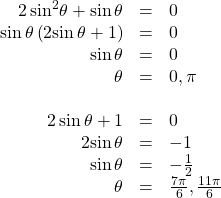
Analysis
We can see the solutions on the graph in (Figure 3). On the interval![]() the graph crosses the x-axis four times, at the solutions noted. Notice that trigonometric equations that are in quadratic form can yield up to four solutions instead of the expected two that are found with quadratic equations. In this example, each solution (angle) corresponding to a positive sine value will yield two angles that would result in that value.
the graph crosses the x-axis four times, at the solutions noted. Notice that trigonometric equations that are in quadratic form can yield up to four solutions instead of the expected two that are found with quadratic equations. In this example, each solution (angle) corresponding to a positive sine value will yield two angles that would result in that value.

We can verify the solutions on the unit circle in (Figure) as well.
Solving a Trigonometric Equation Quadratic in Form
Solve the equation quadratic in form exactly:![]()
Show Solution
We can factor using grouping. Solution values of ![]() can be found on the unit circle.
can be found on the unit circle.
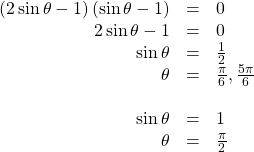
Try It
Solve the quadratic equation ![]()
Show Solution
![]()
Solving Trigonometric Equations Using Fundamental Identities
While algebra can be used to solve a number of trigonometric equations, we can also use the fundamental identities because they make solving equations simpler. Remember that the techniques we use for solving are not the same as those for verifying identities. The basic rules of algebra apply here, as opposed to rewriting one side of the identity to match the other side. In the next example, we use two identities to simplify the equation.
Use Identities to Solve an Equation
Use identities to solve exactly the trigonometric equation over the interval![]()
Show Solution
Notice that the left side of the equation is the difference formula for cosine.
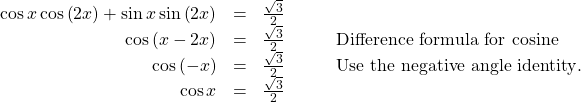
From the unit circle in (Figure), we see that ![]() when
when ![]()
Solving the Equation Using a Double-Angle Formula
Solve the equation exactly using a double-angle formula:![]() Note: if no mode is specified or implied in context, assume radian mode.
Note: if no mode is specified or implied in context, assume radian mode.
Show Solution
We have three choices of expressions to substitute for the double-angle of cosine. As it is simpler to solve for one trigonometric function at a time, we will choose the double-angle identity involving only cosine:
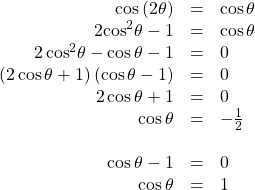
So, if![]() then
then![]() and
and ![]() if
if![]() then
then![]()
Solving an Equation Using an Identity
Solve the equation exactly using an identity: ![]()
Show Solution
If we rewrite the right side, we can write the equation in terms of cosine:
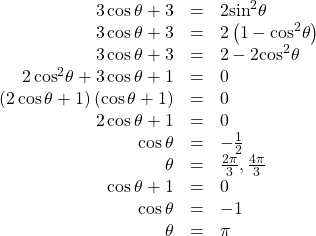
Our solutions are ![]()
Solving Trigonometric Equations with Multiple Angles
Sometimes it is not possible to solve a trigonometric equation with identities that have a multiple angle, such as ![]() or
or ![]() When confronted with these equations, recall that
When confronted with these equations, recall that ![]() is a horizontal compression by a factor of 2 of the function
is a horizontal compression by a factor of 2 of the function ![]() On an interval of
On an interval of ![]() we can graph two periods of
we can graph two periods of ![]() as opposed to one cycle of
as opposed to one cycle of ![]() This compression of the graph leads us to believe there may be twice as many x-intercepts or solutions to
This compression of the graph leads us to believe there may be twice as many x-intercepts or solutions to ![]() compared to
compared to![]() This information will help us solve the equation.
This information will help us solve the equation.
Solving a Multiple Angle Trigonometric Equation
Solve exactly: ![]() on
on ![]()
Show Solution
We can see that this equation is the standard equation with a multiple of an angle. If ![]() we know
we know ![]() is in quadrants I and IV. While
is in quadrants I and IV. While ![]() will only yield solutions in quadrants I and II, we recognize that the solutions to the equation
will only yield solutions in quadrants I and II, we recognize that the solutions to the equation ![]() will be in quadrants I and IV.
will be in quadrants I and IV.
Therefore, the possible angles are ![]() and
and ![]() So,
So,![]() or
or![]() which means that
which means that ![]() or
or ![]() Does this make sense? Yes, because
Does this make sense? Yes, because ![]()
Are there any other possible answers? Let us return to our first step.
In quadrant I, ![]() so
so ![]() as noted. Let us revolve around the circle again:
as noted. Let us revolve around the circle again:
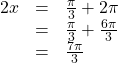
so ![]()
One more rotation yields
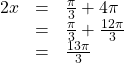
![]() so this value for
so this value for ![]() is larger than
is larger than![]() so it is not a solution on
so it is not a solution on ![]()
In quadrant IV, ![]() so
so ![]() as noted. Let us revolve around the circle again:
as noted. Let us revolve around the circle again:
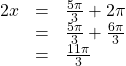
so ![]()
One more rotation yields
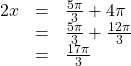
![]() so this value for
so this value for![]() is larger than
is larger than ![]() so it is not a solution on
so it is not a solution on ![]()
Our solutions are ![]() Note that whenever we solve a problem in the form of
Note that whenever we solve a problem in the form of ![]() we must go around the unit circle
we must go around the unit circle ![]() times.
times.
Solving Right Triangle Problems
We can now use all of the methods we have learned to solve problems that involve applying the properties of right triangles and the Pythagorean Theorem. We begin with the familiar Pythagorean Theorem, ![]() and model an equation to fit a situation.
and model an equation to fit a situation.
Using the Pythagorean Theorem to Model an Equation
Use the Pythagorean Theorem, and the properties of right triangles to model an equation that fits the problem.
One of the cables that anchors the center of the London Eye Ferris wheel to the ground must be replaced. The center of the Ferris wheel is 69.5 meters above the ground, and the second anchor on the ground is 23 meters from the base of the Ferris wheel. Approximately how long is the cable, and what is the angle of elevation (from ground up to the center of the Ferris wheel)? Round your solutions to two decimal places. See (Figure 4).

Show Solution
Using the information given, we can draw a right triangle. We can find the length of the cable with the Pythagorean Theorem.
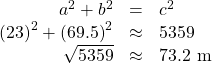
The angle of elevation is ![]() formed by the second anchor on the ground and the cable reaching to the center of the wheel. We can use the tangent function to find its measure. Round to two decimal places.
formed by the second anchor on the ground and the cable reaching to the center of the wheel. We can use the tangent function to find its measure. Round to two decimal places.
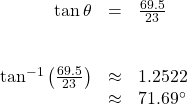
The angle of elevation is approximately ![]() and the length of the cable is 73.2 meters.
and the length of the cable is 73.2 meters.
Using the Pythagorean Theorem to Model an Abstract Problem
OSHA safety regulations require that the base of a ladder be placed 1 foot from the wall for every 4 feet of ladder length. Find the angle that a ladder of any length forms with the ground and the height at which the ladder touches the wall.
Show Solution
For any length of ladder, the base needs to be a distance from the wall equal to one fourth of the ladder’s length. Equivalently, if the base of the ladder is “a” feet from the wall, the length of the ladder will be 4a feet. See (Figure 5).

The side adjacent to ![]() is a and the hypotenuse is
is a and the hypotenuse is ![]() Thus,
Thus,
The elevation of the ladder forms an angle of ![]() with the ground. The height at which the ladder touches the wall can be found using the Pythagorean Theorem:
with the ground. The height at which the ladder touches the wall can be found using the Pythagorean Theorem:
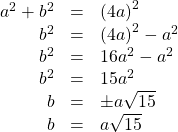
Thus, the ladder touches the wall at ![]() feet from the ground.
feet from the ground.
Access these online resources for additional instruction and practice with solving trigonometric equations.
Key Concepts
- When solving linear trigonometric equations, we can use algebraic techniques just as we do solving algebraic equations. Look for patterns, like the difference of squares, quadratic form, or an expression that lends itself well to substitution. See (Figure), (Figure), and (Figure).
- Equations involving a single trigonometric function can be solved or verified using the unit circle. See (Figure), (Figure), and (Figure), and (Figure).
- We can also solve trigonometric equations using a graphing calculator. See (Figure) and (Figure).
- Many equations appear quadratic in form. We can use substitution to make the equation appear simpler, and then use the same techniques we use solving an algebraic quadratic: factoring, the quadratic formula, etc. See (Figure), (Figure), (Figure), and (Figure).
- We can also use the identities to solve trigonometric equation. See (Figure), (Figure), and (Figure).
- We can use substitution to solve a multiple-angle trigonometric equation, which is a compression of a standard trigonometric function. We will need to take the compression into account and verify that we have found all solutions on the given interval. See (Figure).
- Real-world scenarios can be modeled and solved using the Pythagorean Theorem and trigonometric functions. See (Figure).
Section Exercises
Verbal
Will there always be solutions to trigonometric function equations? If not, describe an equation that would not have a solution. Explain why or why not.
Show Solution
There will not always be solutions to trigonometric function equations. For a basic example, ![]()
When solving a trigonometric equation involving more than one trigonometric function, do we always want to try to rewrite the equation so it is expressed in terms of one trigonometric function? Why or why not?
When solving linear trigonometric equations in terms of only sine or cosine, how do we know whether there will be solutions?
Show Solution
If the sine or cosine function has a coefficient of one, isolate the term on one side of the equals sign. If the number it is set equal to has an absolute value less than or equal to one, the equation has solutions, otherwise it does not. If the sine or cosine does not have a coefficient equal to one, still isolate the term but then divide both sides of the equation by the leading coefficient. Then, if the number it is set equal to has an absolute value greater than one, the equation has no solution.
Algebraic
For the following exercises, find all solutions exactly.
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
For the following exercises, solve exactly on![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
For the following exercises, find all exact solutions on![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
For the following exercises, solve with the methods shown in this section exactly on the interval![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
For the following exercises, solve exactly on the interval![]() Use the quadratic formula if the equations do not factor.
Use the quadratic formula if the equations do not factor.
![]()
Show Solution
![]()
![]()
![]()
Show Solution
There are no solutions.
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
There are no solutions.
For the following exercises, find exact solutions on the interval![]() Look for opportunities to use trigonometric identities.
Look for opportunities to use trigonometric identities.
![]()
![]()
Show Solution
There are no solutions.
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
Graphical
For the following exercises, algebraically determine all solutions of the trigonometric equation exactly, then verify the results by graphing the equation and finding the zeros.
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
There are no solutions.
![]()
![]()
Show Solution
![]()
![]()
Technology
For the following exercises, use a calculator to find all radian solutions to four decimal places.
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
For the following exercises, solve the equations algebraically, and then use a calculator to find the values on the interval![]() Round to four decimal places.
Round to four decimal places.
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
Extensions
For the following exercises, find all solutions exactly to the equations on the interval ![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
There are no solutions.
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
There are no solutions.
![]()
Real-World Applications
For the following exercises, round to two decimal places.
An airplane has only enough gas to fly to a city 200 miles northeast of its current location. If the pilot knows that the city is 25 miles north, how many degrees north of east should the airplane fly?
Show Solution
![]()
If a loading ramp is placed next to a truck, at a height of 4 feet, and the ramp is 15 feet long, what angle does the ramp make with the ground?
If a loading ramp is placed next to a truck, at a height of 2 feet, and the ramp is 20 feet long, what angle does the ramp make with the ground?
Show Solution
![]()
A woman is watching a launched rocket currently 11 miles in altitude. If she is standing 4 miles from the launch pad, at what angle is she looking up from horizontal?
An astronaut is in a launched rocket currently 15 miles in altitude. If a man is standing 2 miles from the launch pad, at what angle is she looking down at him from horizontal? (Hint: this is called the angle of depression.)
Show Solution
![]()
A woman is standing 8 meters away from a 10-meter tall building. At what angle is she looking to the top of the building?
A man is standing 10 meters away from a 6-meter tall building. Someone at the top of the building is looking down at him. At what angle is the person looking at him?
Show Solution
![]()
A 20-foot tall building has a shadow that is 55 feet long. What is the angle of elevation of the sun?
A 90-foot tall building has a shadow that is 2 feet long. What is the angle of elevation of the sun?
Show Solution
![]()
A spotlight on the ground 3 meters from a 2-meter tall man casts a 6 meter shadow on a wall 6 meters from the man. At what angle is the light?
A spotlight on the ground 3 feet from a 5-foot tall woman casts a 15-foot tall shadow on a wall 6 feet from the woman. At what angle is the light?
Show Solution
![]()
For the following exercises, find a solution to the following word problem algebraically. Then use a calculator to verify the result. Round the answer to the nearest tenth of a degree.
A person does a handstand with his feet touching a wall and his hands 1.5 feet away from the wall. If the person is 6 feet tall, what angle do his feet make with the wall?
A person does a handstand with her feet touching a wall and her hands 3 feet away from the wall. If the person is 5 feet tall, what angle do her feet make with the wall?
Show Solution
![]()
A 23-foot ladder is positioned next to a house. If the ladder slips at 7 feet from the house when there is not enough traction, what angle should the ladder make with the ground to avoid slipping?
Chapter Review Exercises
Solving Trigonometric Equations with Identities
For the following exercises, find all solutions exactly that exist on the interval ![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
For the following exercises, use basic identities to simplify the expression.
![]()
Show Solution
![]()
![]()
For the following exercises, determine if the given identities are equivalent.
![]()
Show Solution
Yes
![]()
Sum and Difference Identities
For the following exercises, find the exact value.
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
For the following exercises, prove the identity.
![]()
Show Solution
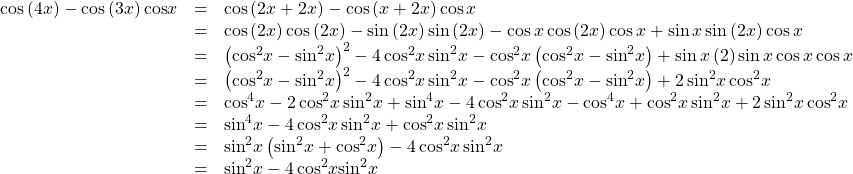
![]()
For the following exercise, simplify the expression.
![]()
Show Solution
![]()
For the following exercises, find the exact value.
![]()
![]()
Show Solution
![]()
Double-Angle, Half-Angle, and Reduction Formulas
For the following exercises, find the exact value.
Find ![]() and
and ![]() given
given ![]() and
and ![]() is in the interval
is in the interval ![]()
Find ![]() and
and ![]() given
given ![]() and
and ![]() is in the interval
is in the interval ![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
For the following exercises, use (Figure 6) to find the desired quantities.

![]()
![]()
Show Solution
![]()
For the following exercises, prove the identity.
![]()
Show Solution
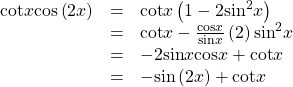
For the following exercises, rewrite the expression with no powers.
![]()
![]()
Show Solution
![]()
Sum-to-Product and Product-to-Sum Formulas
For the following exercises, evaluate the product for the given expression using a sum or difference of two functions. Write the exact answer.
![]()
![]()
Show Solution
![]()
![]()
For the following exercises, evaluate the sum by using a product formula. Write the exact answer.
![]()
Show Solution
![]()
![]()
For the following exercises, change the functions from a product to a sum or a sum to a product.
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
Solving Trigonometric Equations
For the following exercises, find all exact solutions on the interval ![]()
![]()
Show Solution
![]()
![]()
For the following exercises, find all exact solutions on the interval ![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
No solution
For the following exercises, simplify the equation algebraically as much as possible. Then use a calculator to find the solutions on the interval ![]() Round to four decimal places.
Round to four decimal places.
![]()
![]()
Show Solution
![]()
For the following exercises, graph each side of the equation to find the approximate solutions on the interval ![]()
![]()
![]()
Show Solution
![]()
Practice Test
For the following exercises, simplify the given expression.
![]()
Show Solution
1
![]()
![]()
Show Solution
![]()
![]()
Show Solution
1
For the following exercises, find the exact value.
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
Show Solution
![]()
For the following exercises, simplify each expression. Do not evaluate.
![]()
Show Solution
![]()
![]()
Show Solution
![]()
For the following exercises, find all exact solutions to the equation on ![]()
![]()
Show Solution
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
Rewrite the expression as a product instead of a sum:![]()
For the following exercise, rewrite the product as a sum or difference.
![]()
Show Solution
![]()
For the following exercise, rewrite the sum or difference as a product.
![]()
Show Solution
![]()
Find all solutions of ![]()
Show Solution
![]()
Find the solutions of ![]() on the interval
on the interval ![]() algebraically; then graph both sides of the equation to determine the answer.
algebraically; then graph both sides of the equation to determine the answer.
For the following exercises, find all solutions exactly on the interval ![]()
![]()
Show Solution
![]()
![]()
Show Solution
![]()
Find ![]() and
and ![]() given
given ![]() and
and ![]() is on the interval
is on the interval![]()
Show Solution
![]()
Find ![]() and
and ![]() given
given ![]() and
and ![]() is in quadrant IV.
is in quadrant IV.
Rewrite the expression ![]() with no powers greater than 1.
with no powers greater than 1.
Show Solution
![]()
For the following exercises, prove the identity.
![]()
![]()
Show Solution
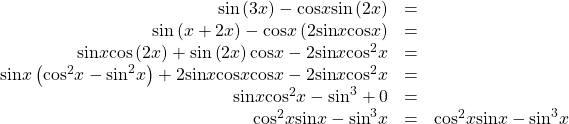
![]()
Plot the points and find a function of the form![]() that fits the given data.
that fits the given data.
Show Solution
![]()
The displacement ![]() in centimeters of a mass suspended by a spring is modeled by the function
in centimeters of a mass suspended by a spring is modeled by the function![]() where
where![]() is measured in seconds. Find the amplitude, period, and frequency of this displacement.
is measured in seconds. Find the amplitude, period, and frequency of this displacement.
A woman is standing 300 feet away from a 2,000-foot building. If she looks to the top of the building, at what angle above horizontal is she looking? A bored worker looks down at her from the 15th floor (1,500 feet above her). At what angle is he looking down at her? Round to the nearest tenth of a degree.
Show Solution
![]()
Two frequencies of sound are played on an instrument governed by the equation![]() What are the period and frequency of the “fast” and “slow” oscillations? What is the amplitude?
What are the period and frequency of the “fast” and “slow” oscillations? What is the amplitude?
The average monthly snowfall in a small village in the Himalayas is 6 inches, with the low of 1 inch occurring in July. Construct a function that models this behavior. During what period is there more than 10 inches of snowfall?
Show Solution
![]() . From November 23 to February 6.
. From November 23 to February 6.
A spring attached to a ceiling is pulled down 20 cm. After 3 seconds, wherein it completes 6 full periods, the amplitude is only 15 cm. Find the function modeling the position of the spring![]() seconds after being released. At what time will the spring come to rest? In this case, use 1 cm amplitude as rest.
seconds after being released. At what time will the spring come to rest? In this case, use 1 cm amplitude as rest.
Water levels near a glacier currently average 9 feet, varying seasonally by 2 inches above and below the average and reaching their highest point in January. Due to global warming, the glacier has begun melting faster than normal. Every year, the water levels rise by a steady 3 inches. Find a function modeling the depth of the water![]() months from now. If the docks are 2 feet above current water levels, at what point will the water first rise above the docks?
months from now. If the docks are 2 feet above current water levels, at what point will the water first rise above the docks?
Show Solution
![]() 93.5855 months (or 7.8 years) from now
93.5855 months (or 7.8 years) from now
