11 Solving Trigonometric Equations with Identities
Learning Objectives
In this section, you will:
- Verify the fundamental trigonometric identities.
- Simplify trigonometric expressions using algebra and the identities.

In espionage movies, we see international spies with multiple passports, each claiming a different identity. However, we know that each of those passports represents the same person. The trigonometric identities act in a similar manner to multiple passports—there are many ways to represent the same trigonometric expression. Just as a spy will choose an Italian passport when traveling to Italy, we choose the identity that applies to the given scenario when solving a trigonometric equation.
In this section, we will begin an examination of the fundamental trigonometric identities, including how we can verify them and how we can use them to simplify trigonometric expressions.
Verifying the Fundamental Trigonometric Identities
Identities enable us to simplify complicated expressions. They are the basic tools of trigonometry used in solving trigonometric equations, just as factoring, finding common denominators, and using special formulas are the basic tools of solving algebraic equations. In fact, we use algebraic techniques constantly to simplify trigonometric expressions. Basic properties and formulas of algebra, such as the difference of squares formula and the perfect squares formula, will simplify the work involved with trigonometric expressions and equations. We already know that all of the trigonometric functions are related because they all are defined in terms of the unit circle. Consequently, any trigonometric identity can be written in many ways.
To verify the trigonometric identities, we usually start with the more complicated side of the equation and essentially rewrite the expression until it has been transformed into the same expression as the other side of the equation. Sometimes we have to factor expressions, expand expressions, find common denominators, or use other algebraic strategies to obtain the desired result. In this first section, we will work with the fundamental identities: the Pythagorean identities, the even-odd identities, the reciprocal identities, and the quotient identities.
We will begin with the Pythagorean identities (see (Figure)), which are equations involving trigonometric functions based on the properties of a right triangle. We have already seen and used the first of these identifies, but now we will also use additional identities.
| Pythagorean Identities | ||
|---|---|---|
The second and third identities can be obtained by manipulating the first. The identity![]() is found by rewriting the left side of the equation in terms of sine and cosine.
is found by rewriting the left side of the equation in terms of sine and cosine.
Prove:![]()

Similarly,![]() can be obtained by rewriting the left side of this identity in terms of sine and cosine. This gives
can be obtained by rewriting the left side of this identity in terms of sine and cosine. This gives

Recall that we determined which trigonometric functions are odd and which are even. The next set of fundamental identities is the set of even-odd identities. The even-odd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle. (See (Figure)).
| Even-Odd Identities | ||
|---|---|---|
Recall that an odd function is one in which ![]() for all
for all ![]() in the domain of
in the domain of![]() The sine function is an odd function because
The sine function is an odd function because ![]() The graph of an odd function is symmetric about the origin. For example, consider corresponding inputs of
The graph of an odd function is symmetric about the origin. For example, consider corresponding inputs of ![]() and
and ![]() The output of
The output of ![]() is opposite the output of
is opposite the output of ![]() Thus,
Thus,
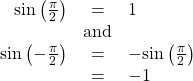
This is shown in (Figure 2).
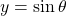
Recall that an even function is one in which
The graph of an even function is symmetric about the y-axis. The cosine function is an even function because ![]()
For example, consider corresponding inputs ![]() and
and ![]() The output of
The output of ![]() is the same as the output of
is the same as the output of ![]() Thus,
Thus,
See (Figure 3).
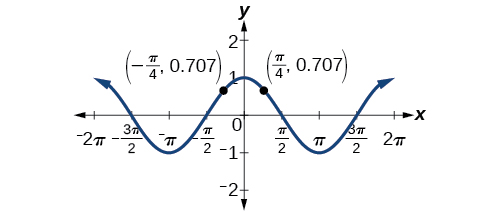
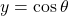
For all ![]() in the domain of the sine and cosine functions, respectively, we can state the following:
in the domain of the sine and cosine functions, respectively, we can state the following:
- Since
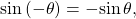 sine is an odd function.
sine is an odd function. - Since
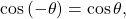 cosine is an even function.
cosine is an even function.
The other even-odd identities follow from the even and odd nature of the sine and cosine functions. For example, consider the tangent identity, ![]() We can interpret the tangent of a negative angle as
We can interpret the tangent of a negative angle as![]() Tangent is therefore an odd function, which means that
Tangent is therefore an odd function, which means that ![]() for all
for all ![]() in the domain of the tangent function.
in the domain of the tangent function.
The cotangent identity,![]() also follows from the sine and cosine identities. We can interpret the cotangent of a negative angle as
also follows from the sine and cosine identities. We can interpret the cotangent of a negative angle as![]() Cotangent is therefore an odd function, which means that
Cotangent is therefore an odd function, which means that![]() for all
for all![]() in the domain of the cotangent function.
in the domain of the cotangent function.
The cosecant function is the reciprocal of the sine function, which means that the cosecant of a negative angle will be interpreted as![]() The cosecant function is therefore odd.
The cosecant function is therefore odd.
Finally, the secant function is the reciprocal of the cosine function, and the secant of a negative angle is interpreted as![]() The secant function is therefore even.
The secant function is therefore even.
To sum up, only two of the trigonometric functions, cosine and secant, are even. The other four functions are odd, verifying the even-odd identities.
The next set of fundamental identities is the set of reciprocal identities, which, as their name implies, relate trigonometric functions that are reciprocals of each other. See (Figure). Recall that we first encountered these identities when defining trigonometric functions from right angles in Right Angle Trigonometry.
| Reciprocal Identities | |
|---|---|
The final set of fundamental identities is the set of quotient identities, which define relationships among certain trigonometric functions and can be very helpful in verifying other identities. See (Figure).
| Quotient Identities | |
|---|---|
The reciprocal and quotient identities are derived from the definitions of the basic fundamental trigonometric functions.
Summarizing Fundamental Trigonometric Identities
The Pythagorean identities are based on the properties of a right triangle.
The even-odd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle.
The reciprocal identities define reciprocals of the trigonometric functions.
The quotient identities define the relationship among the trigonometric functions.
Graphing the Equations of an Identity
Graph both sides of the identity ![]() In other words, on the graphing calculator, graph
In other words, on the graphing calculator, graph ![]() and
and ![]()
Analysis
We see only one graph because both expressions generate the same image. One is on top of the other. This is a good way to confirm an identity verified with analytical means. If both expressions give the same graph, then they are most likely identities.
How To
Given a trigonometric identity, verify that it is true.
- Work on one side of the equation. It is usually better to start with the more complex side, as it is easier to simplify than to build.
- Look for opportunities to factor expressions, square a binomial, multiply by the conjugate, or add fractions.
- Noting which functions are in the final expression, look for opportunities to use the identities and make the proper substitutions.
- If these steps do not yield the desired result, try converting all terms to sines and cosines.
Verifying a Trigonometric Identity
Verify ![]()
Show Solution
We will start on the left side, as it is the more complicated side:
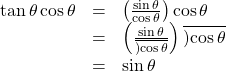
Analysis
This identity was fairly simple to verify, as it only required writing![]() in terms of
in terms of![]() and
and![]()
Try It
Verify the identity![]()
Show Solution
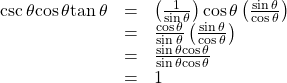
Verifying the Equivalency Using the Even-Odd Identities
Verify the following equivalency using the even-odd identities:
Show Solution
Working on the left side of the equation, we have
![Rendered by QuickLaTeX.com \begin{array}{cccc}\hfill \left(1+\mathrm{sin}\,x\right)\left[1+\mathrm{sin}\left(-x\right)\right]& =& \left(1+\mathrm{sin}\,x\right)\left(1-\mathrm{sin}\,x\right)\hfill & \phantom{\rule{1em}{0ex}}\text{Since sin(−}x\text{)=}-\mathrm{sin}\,x\hfill \\ & =& 1-{\mathrm{sin}}^{2}x\hfill & \phantom{\rule{1em}{0ex}}\text{Difference of squares}\hfill \\ & =& {\mathrm{cos}}^{2}x\hfill & {\phantom{\rule{1em}{0ex}}\text{cos}}^{2}x=1-{\mathrm{sin}}^{2}x\hfill \end{array}](https://university.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-1702bf2efa9c49daeeffb170042198ca_l3.png)
Verifying a Trigonometric Identity Involving sec2θ
Verify the identity ![]()
Show Solution
As the left side is more complicated, let’s begin there.
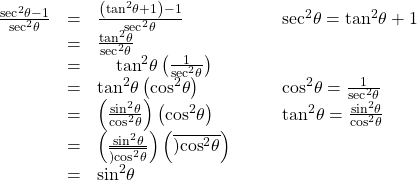
There is more than one way to verify an identity. Here is another possibility. Again, we can start with the left side.
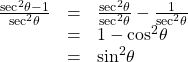
Analysis
In the first method, we used the identity ![]() and continued to simplify. In the second method, we split the fraction, putting both terms in the numerator over the common denominator. This problem illustrates that there are multiple ways we can verify an identity. Employing some creativity can sometimes simplify a procedure. As long as the substitutions are correct, the answer will be the same.
and continued to simplify. In the second method, we split the fraction, putting both terms in the numerator over the common denominator. This problem illustrates that there are multiple ways we can verify an identity. Employing some creativity can sometimes simplify a procedure. As long as the substitutions are correct, the answer will be the same.
Try It
Show that ![]()
Show Solution
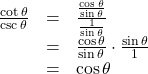
Creating and Verifying an Identity
Create an identity for the expression ![]() by rewriting strictly in terms of sine.
by rewriting strictly in terms of sine.
Show Solution
There are a number of ways to begin, but here we will use the quotient and reciprocal identities to rewrite the expression:
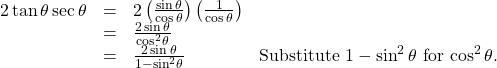
Thus,
Verifying an Identity Using Algebra and Even/Odd Identities
Verify the identity:
Show Solution
Let’s start with the left side and simplify:
![Rendered by QuickLaTeX.com \begin{array}{cccc}\hfill \frac{{\mathrm{sin}}^{2}\left(-\theta \right)-{\mathrm{cos}}^{2}\left(-\theta \right)}{\mathrm{sin}\left(-\theta \right)-\mathrm{cos}\left(-\theta \right)}& =& \frac{{\left[\mathrm{sin}\left(-\theta \right)\right]}^{2}-{\left[\mathrm{cos}\left(-\theta \right)\right]}^{2}}{\mathrm{sin}\left(-\theta \right)-\mathrm{cos}\left(-\theta \right)}\hfill & \\ & =& \frac{{\left(-\mathrm{sin}\,\theta \right)}^{2}-{\left(\mathrm{cos}\,\theta \right)}^{2}}{-\mathrm{sin}\,\theta -\mathrm{cos}\,\theta }\hfill & \phantom{\rule{1em}{0ex}}\mathrm{sin}\left(-x\right)=-\mathrm{sin}\,x\,\text{and}\,\mathrm{cos}\left(-x\right)=\mathrm{cos}\,x\hfill \\ & =& \frac{{\left(\mathrm{sin}\,\theta \right)}^{2}-{\left(\mathrm{cos}\,\theta \right)}^{2}}{-\mathrm{sin}\,\theta -\mathrm{cos}\,\theta }\hfill & \phantom{\rule{1em}{0ex}}\text{Difference of squares}\hfill \\ & =& \frac{\left(\mathrm{sin}\,\theta -\mathrm{cos}\,\theta \right)\left(\mathrm{sin}\,\theta +\mathrm{cos}\,\theta \right)}{-\left(\mathrm{sin}\,\theta +\mathrm{cos}\,\theta \right)}\hfill & \\ & =& \frac{\left(\mathrm{sin}\,\theta -\mathrm{cos}\,\theta \right)\left(\overline{)\mathrm{sin}\,\theta +\mathrm{cos}\,\theta }\right)}{-\left(\overline{)\mathrm{sin}\,\theta +\mathrm{cos}\,\theta }\right)}\hfill & \\ & =& \mathrm{cos}\,\theta -\mathrm{sin}\,\theta \hfill & \end{array}](https://university.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-246376b45ef975a3be710d3aef2385aa_l3.png)
Try It
Verify the identity ![]()
Show Solution
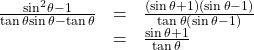
Verifying an Identity Involving Cosines and Cotangents
Verify the identity:![]()
Show Solution
We will work on the left side of the equation.
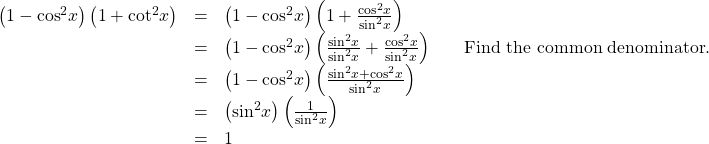
Using Algebra to Simplify Trigonometric Expressions
We have seen that algebra is very important in verifying trigonometric identities, but it is just as critical in simplifying trigonometric expressions before solving. Being familiar with the basic properties and formulas of algebra, such as the difference of squares formula, the perfect square formula, or substitution, will simplify the work involved with trigonometric expressions and equations.
For example, the equation ![]() resembles the equation
resembles the equation![]() which uses the factored form of the difference of squares. Using algebra makes finding a solution straightforward and familiar. We can set each factor equal to zero and solve. This is one example of recognizing algebraic patterns in trigonometric expressions or equations.
which uses the factored form of the difference of squares. Using algebra makes finding a solution straightforward and familiar. We can set each factor equal to zero and solve. This is one example of recognizing algebraic patterns in trigonometric expressions or equations.
Another example is the difference of squares formula, ![]() which is widely used in many areas other than mathematics, such as engineering, architecture, and physics. We can also create our own identities by continually expanding an expression and making the appropriate substitutions. Using algebraic properties and formulas makes many trigonometric equations easier to understand and solve.
which is widely used in many areas other than mathematics, such as engineering, architecture, and physics. We can also create our own identities by continually expanding an expression and making the appropriate substitutions. Using algebraic properties and formulas makes many trigonometric equations easier to understand and solve.
Writing the Trigonometric Expression as an Algebraic Expression
Write the following trigonometric expression as an algebraic expression:![]()
Show Solution
Notice that the pattern displayed has the same form as a standard quadratic expression, ![]() Letting
Letting ![]() we can rewrite the expression as follows:
we can rewrite the expression as follows:
This expression can be factored as ![]() If it were set equal to zero and we wanted to solve the equation, we would use the zero factor property and solve each factor for
If it were set equal to zero and we wanted to solve the equation, we would use the zero factor property and solve each factor for ![]() At this point, we would replace
At this point, we would replace ![]() with
with ![]() and solve for
and solve for ![]()
Factor a Trigonometric Expression Using the Difference of Squares
Rewrite the trigonometric expression using the difference of squares:![]()
Show Solution
Notice that both the coefficient and the trigonometric expression in the first term are squared, and in the second term the square of the number 1 is 1. This is the difference of squares.
Analysis
If this expression were written in the form of an equation set equal to zero, we could solve each factor using the zero factor property. We could also use substitution like we did in the previous problem and let ![]() rewrite the expression as
rewrite the expression as ![]() and factor
and factor ![]() Then replace
Then replace![]() with
with ![]() and solve for the angle.
and solve for the angle.
Try It
Rewrite the trigonometric expression using the difference of squares:![]()
Show Solution
This is a difference of squares formula:![]()
Simplify by Rewriting and Using Substitution
Simplify the expression by rewriting and using identities:
Show Solution
We can start with the Pythagorean identity.
Now we can simplify by substituting ![]() for
for ![]() We have
We have
Try It
Use algebraic techniques to verify the identity: ![]()
(Hint: Multiply the numerator and denominator on the left side by![]()
Show Solution
Access these online resources for additional instruction and practice with the fundamental trigonometric identities.
Key Equations
| Pythagorean identities | 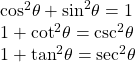 |
| Even-odd identities | 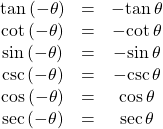 |
| Reciprocal identities | 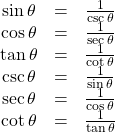 |
| Quotient identities |
Key Concepts
- There are multiple ways to represent a trigonometric expression. Verifying the identities illustrates how expressions can be rewritten to simplify a problem.
- Graphing both sides of an identity will verify it. See (Figure).
- Simplifying one side of the equation to equal the other side is another method for verifying an identity. See (Figure) and (Figure).
- The approach to verifying an identity depends on the nature of the identity. It is often useful to begin on the more complex side of the equation. See (Figure).
- We can create an identity and then verify it. See (Figure).
- Verifying an identity may involve algebra with the fundamental identities. See (Figure) and (Figure).
- Algebraic techniques can be used to simplify trigonometric expressions. We use algebraic techniques throughout this text, as they consist of the fundamental rules of mathematics. See (Figure), (Figure), and (Figure).
Section Exercises
Verbal
We know ![]() is an even function, and
is an even function, and![]() and
and ![]() are odd functions. What about
are odd functions. What about ![]() and
and ![]() Are they even, odd, or neither? Why?
Are they even, odd, or neither? Why?
Show Solution
All three functions,![]() and
and![]() are even.
are even.
This is because ![]() and
and![]()
Examine the graph of ![]() on the interval
on the interval ![]() How can we tell whether the function is even or odd by only observing the graph of
How can we tell whether the function is even or odd by only observing the graph of![]()
After examining the reciprocal identity for ![]() explain why the function is undefined at certain points.
explain why the function is undefined at certain points.
Show Solution
When ![]() then
then ![]() which is undefined.
which is undefined.
All of the Pythagorean identities are related. Describe how to manipulate the equations to get from ![]() to the other forms.
to the other forms.
Algebraic
For the following exercises, use the fundamental identities to fully simplify the expression.
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
For the following exercises, simplify the first trigonometric expression by writing the simplified form in terms of the second expression.
![]() , in terms of
, in terms of ![]()
![]() , in terms of
, in terms of ![]()
Show Solution
![]()
![]() , in terms of
, in terms of ![]()
![]() , in terms of
, in terms of ![]()
Show Solution
![]()
![]() , in terms of
, in terms of ![]()
![]() , in terms of
, in terms of ![]()
Show Solution
![]()
![]() , in terms of
, in terms of ![]()
![]() , in terms of
, in terms of ![]()
Show Solution
![]()
![]() in terms of
in terms of ![]()
![]() in terms of
in terms of ![]()
Show Solution
![]()
![]() in terms of
in terms of ![]()
![]() in terms of
in terms of ![]()
Show Solution
![]()
![]() , in terms of
, in terms of ![]()
For the following exercises, verify the identity.
![]()
Show Solution
Answers will vary. Sample proof:
![]()
![]()
![]()
Show Solution
Answers will vary. Sample proof:
![]()
![]()
Show Solution
Answers will vary. Sample proof:
![]()
Extensions
For the following exercises, prove or disprove the identity.
![]()
![]()
Show Solution
False
![]()
![]()
Show Solution
False
![]()
![]()
Show Solution
Proved with negative and Pythagorean identities
For the following exercises, determine whether the identity is true or false. If false, find an appropriate equivalent expression.
![]()
![]()
Show Solution
True![]()
![]()
Glossary
- even-odd identities
- set of equations involving trigonometric functions such that if
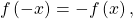 the identity is odd, and if
the identity is odd, and if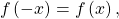 the identity is even
the identity is even
- Pythagorean identities
- set of equations involving trigonometric functions based on the right triangle properties
- quotient identities
- pair of identities based on the fact that tangent is the ratio of sine and cosine, and cotangent is the ratio of cosine and sine
- reciprocal identities
- set of equations involving the reciprocals of basic trigonometric definitions