13 Double-Angle, Half-Angle, and Reduction Formulas
Learning Objectives
In this section, you will:
- Use double-angle formulas to find exact values.
- Use double-angle formulas to verify identities.
- Use reduction formulas to simplify an expression.
- Use half-angle formulas to find exact values.

Bicycle ramps made for competition (see (Figure 1)) must vary in height depending on the skill level of the competitors. For advanced competitors, the angle formed by the ramp and the ground should be ![]() such that
such that ![]() The angle is divided in half for novices. What is the steepness of the ramp for novices? In this section, we will investigate three additional categories of identities that we can use to answer questions such as this one.
The angle is divided in half for novices. What is the steepness of the ramp for novices? In this section, we will investigate three additional categories of identities that we can use to answer questions such as this one.
Using Double-Angle Formulas to Find Exact Values
In the previous section, we used addition and subtraction formulas for trigonometric functions. Now, we take another look at those same formulas. The double-angle formulas are a special case of the sum formulas, where![]() Deriving the double-angle formula for sine begins with the sum formula,
Deriving the double-angle formula for sine begins with the sum formula,
If we let ![]() then we have
then we have
Deriving the double-angle for cosine gives us three options. First, starting from the sum formula, ![]() and letting
and letting ![]() we have
we have
Using the Pythagorean properties, we can expand this double-angle formula for cosine and get two more variations. The first variation is:
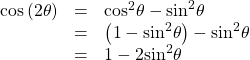
The second variation is:
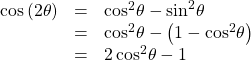
Similarly, to derive the double-angle formula for tangent, replacing ![]() in the sum formula gives
in the sum formula gives
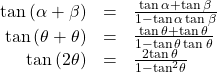
Double-Angle Formulas
The double-angle formulas are summarized as follows:
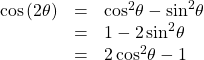
How To
Given the tangent of an angle and the quadrant in which it is located, use the double-angle formulas to find the exact value.
- Draw a triangle to reflect the given information.
- Determine the correct double-angle formula.
- Substitute values into the formula based on the triangle.
- Simplify.
Using a Double-Angle Formula to Find the Exact Value Involving Tangent
Given that ![]() and
and ![]() is in quadrant II, find the following:
is in quadrant II, find the following:
Show Solution
If we draw a triangle to reflect the information given, we can find the values needed to solve the problems on the image. We are given ![]() such that
such that ![]() is in quadrant II. The tangent of an angle is equal to the opposite side over the adjacent side, and because
is in quadrant II. The tangent of an angle is equal to the opposite side over the adjacent side, and because ![]() is in the second quadrant, the adjacent side is on the x-axis and is negative. Use the Pythagorean Theorem to find the length of the hypotenuse:
is in the second quadrant, the adjacent side is on the x-axis and is negative. Use the Pythagorean Theorem to find the length of the hypotenuse:
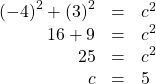
Now we can draw a triangle similar to the one shown in (Figure 2).

- Let’s begin by writing the double-angle formula for sine.
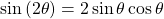
We see that we to need to find
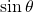 and
and 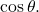 Based on (Figure 2), we see that the hypotenuse equals 5, so
Based on (Figure 2), we see that the hypotenuse equals 5, so 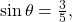 and
and 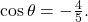 Substitute these values into the equation, and simplify.
Substitute these values into the equation, and simplify.Thus,
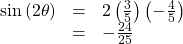
- Write the double-angle formula for cosine.
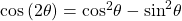
Again, substitute the values of the sine and cosine into the equation, and simplify.
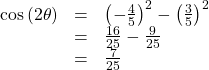
- Write the double-angle formula for tangent.
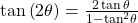
In this formula, we need the tangent, which we were given as
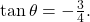 Substitute this value into the equation, and simplify.
Substitute this value into the equation, and simplify.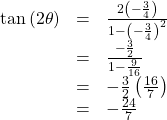
Try It
Given ![]() with
with ![]() in quadrant I, find
in quadrant I, find ![]()
Show Solution
![]()
Using the Double-Angle Formula for Cosine without Exact Values
Use the double-angle formula for cosine to write![]() in terms of
in terms of![]()
Show Solution
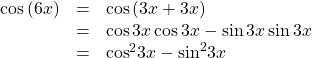
Analysis
This example illustrates that we can use the double-angle formula without having exact values. It emphasizes that the pattern is what we need to remember and that identities are true for all values in the domain of the trigonometric function.
Using Double-Angle Formulas to Verify Identities
Establishing identities using the double-angle formulas is performed using the same steps we used to derive the sum and difference formulas. Choose the more complicated side of the equation and rewrite it until it matches the other side.
Using the Double-Angle Formulas to Verify an Identity
Verify the following identity using double-angle formulas:
Show Solution
We will work on the right side of the equal sign and rewrite the expression until it matches the left side.
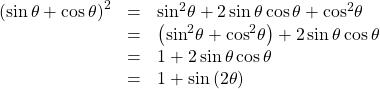
Analysis
This process is not complicated, as long as we recall the perfect square formula from algebra:
where ![]() and
and ![]() Part of being successful in mathematics is the ability to recognize patterns. While the terms or symbols may change, the algebra remains consistent.
Part of being successful in mathematics is the ability to recognize patterns. While the terms or symbols may change, the algebra remains consistent.
Try It
Verify the identity: ![]()
Show Solution
![]()
Verifying a Double-Angle Identity for Tangent
Verify the identity:
Show Solution
In this case, we will work with the left side of the equation and simplify or rewrite until it equals the right side of the equation.

Analysis
Here is a case where the more complicated side of the initial equation appeared on the right, but we chose to work the left side. However, if we had chosen the left side to rewrite, we would have been working backwards to arrive at the equivalency. For example, suppose that we wanted to show
Let’s work on the right side.
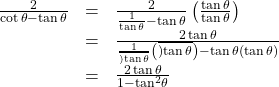
When using the identities to simplify a trigonometric expression or solve a trigonometric equation, there are usually several paths to a desired result. There is no set rule as to what side should be manipulated. However, we should begin with the guidelines set forth earlier.
Try It
Verify the identity: ![]()
Show Solution
![]()
Use Reduction Formulas to Simplify an Expression
The double-angle formulas can be used to derive the reduction formulas, which are formulas we can use to reduce the power of a given expression involving even powers of sine or cosine. They allow us to rewrite the even powers of sine or cosine in terms of the first power of cosine. These formulas are especially important in higher-level math courses, calculus in particular. Also called the power-reducing formulas, three identities are included and are easily derived from the double-angle formulas.
We can use two of the three double-angle formulas for cosine to derive the reduction formulas for sine and cosine. Let’s begin with ![]() Solve for
Solve for ![]()
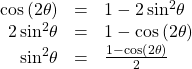
Next, we use the formula![]() Solve for
Solve for![]()
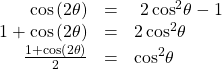
The last reduction formula is derived by writing tangent in terms of sine and cosine:
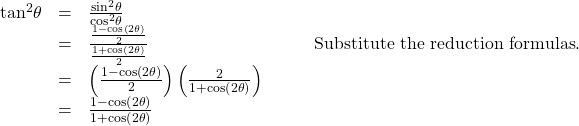
Reduction Formulas
The reduction formulas are summarized as follows:
Writing an Equivalent Expression Not Containing Powers Greater Than 1
Write an equivalent expression for![]() that does not involve any powers of sine or cosine greater than 1.
that does not involve any powers of sine or cosine greater than 1.
Show Solution
We will apply the reduction formula for cosine twice.

Analysis
The solution is found by using the reduction formula twice, as noted, and the perfect square formula from algebra.
Using the Power-Reducing Formulas to Prove an Identity
Use the power-reducing formulas to prove
Show Solution
We will work on simplifying the left side of the equation:
![Rendered by QuickLaTeX.com \begin{array}{cccc}\hfill {\mathrm{sin}}^{3}\left(2x\right)& =& \left[\mathrm{sin}\left(2x\right)\right]\left[{\mathrm{sin}}^{2}\left(2x\right)\right]\hfill & \\ & =& \mathrm{sin}\left(2x\right)\left[\frac{1-\mathrm{cos}\left(4x\right)}{2}\right]\hfill & \text{Substitute the power-reduction formula}.\hfill \\ & =& \mathrm{sin}\left(2x\right)\left(\frac{1}{2}\right)\left[1-\mathrm{cos}\left(4x\right)\right]\hfill & \\ & =& \frac{1}{2}\left[\mathrm{sin}\left(2x\right)\right]\left[1-\mathrm{cos}\left(4x\right)\right]\hfill & \end{array}](https://university.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-736e897e3ce7a1e3f3e9e890f996d0da_l3.png)
Analysis
Note that in this example, we substituted
for ![]() The formula states
The formula states
We let ![]() so
so ![]()
Try It
Use the power-reducing formulas to prove that![]()
Show Solution
![Rendered by QuickLaTeX.com \begin{array}{cccc}\hfill 10{\mathrm{cos}}^{4}x& =& 10{\left({\mathrm{cos}}^{2}x\right)}^{2}\hfill & \\ & =& 10{\left[\frac{1+\mathrm{cos}\left(2x\right)}{2}\right]}^{2}\hfill & {\phantom{\rule{1em}{0ex}}\text{Substitute reduction formula for cos}}^{2}x.\hfill \\ & =& \frac{10}{4}\left[1+2\mathrm{cos}\left(2x\right)+{\mathrm{cos}}^{2}\left(2x\right)\right]\hfill & \\ & =& \frac{10}{4}+\frac{10}{2}\mathrm{cos}\left(2x\right)+\frac{10}{4}\left(\frac{1+\mathrm{cos}2\left(2x\right)}{2}\right)\hfill & {\phantom{\rule{1em}{0ex}}\text{Substitute reduction formula for cos}}^{2}x.\hfill \\ & =& \frac{10}{4}+\frac{10}{2}\mathrm{cos}\left(2x\right)+\frac{10}{8}+\frac{10}{8}\mathrm{cos}\left(4x\right)\hfill & \\ & =& \frac{30}{8}+5\mathrm{cos}\left(2x\right)+\frac{10}{8}\mathrm{cos}\left(4x\right)\hfill & \\ & =& \frac{15}{4}+5\mathrm{cos}\left(2x\right)+\frac{5}{4}\mathrm{cos}\left(4x\right)\hfill & \end{array}](https://university.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-8c5864f822e35ecdb4042785d8aecbb2_l3.png)
Using Half-Angle Formulas to Find Exact Values
The next set of identities is the set of half-angle formulas, which can be derived from the reduction formulas and we can use when we have an angle that is half the size of a special angle. If we replace![]() with
with![]() the half-angle formula for sine is found by simplifying the equation and solving for
the half-angle formula for sine is found by simplifying the equation and solving for![]() Note that the half-angle formulas are preceded by a
Note that the half-angle formulas are preceded by a![]() sign. This does not mean that both the positive and negative expressions are valid. Rather, it depends on the quadrant in which
sign. This does not mean that both the positive and negative expressions are valid. Rather, it depends on the quadrant in which![]() terminates.
terminates.
The half-angle formula for sine is derived as follows:
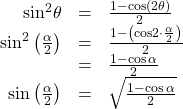
To derive the half-angle formula for cosine, we have
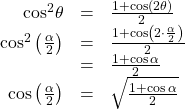
For the tangent identity, we have
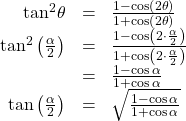
Half-Angle Formulas
The half-angle formulas are as follows:
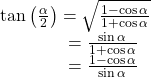
Using a Half-Angle Formula to Find the Exact Value of a Sine Function
Find ![]() using a half-angle formula.
using a half-angle formula.
Show Solution
Since ![]() we use the half-angle formula for sine:
we use the half-angle formula for sine:
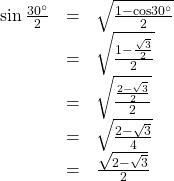
Remember that we can check the answer with a graphing calculator.
Analysis
Notice that we used only the positive root because ![]() is positive.
is positive.
How To
Given the tangent of an angle and the quadrant in which the angle lies, find the exact values of trigonometric functions of half of the angle.
- Draw a triangle to represent the given information.
- Determine the correct half-angle formula.
- Substitute values into the formula based on the triangle.
- Simplify.
Finding Exact Values Using Half-Angle Identities
Given that![]() and
and![]() lies in quadrant III, find the exact value of the following:
lies in quadrant III, find the exact value of the following:
Show Solution
Using the given information, we can draw the triangle shown in (Figure 3). Using the Pythagorean Theorem, we find the hypotenuse to be 17. Therefore, we can calculate ![]() and
and ![]()

- Before we start, we must remember that if
 is in quadrant III, then
is in quadrant III, then 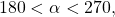 so
so 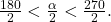 This means that the terminal side of
This means that the terminal side of 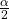 is in quadrant II, since
is in quadrant II, since 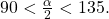
To find
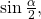 we begin by writing the half-angle formula for sine. Then we substitute the value of the cosine we found from the triangle in (Figure) and simplify.
we begin by writing the half-angle formula for sine. Then we substitute the value of the cosine we found from the triangle in (Figure) and simplify.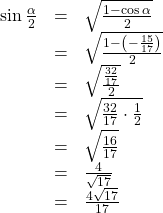
We choose the positive value of
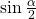 because the angle terminates in quadrant II and sine is positive in quadrant II.
because the angle terminates in quadrant II and sine is positive in quadrant II. - To find
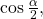 we will write the half-angle formula for cosine, substitute the value of the cosine we found from the triangle in (Figure), and simplify.
we will write the half-angle formula for cosine, substitute the value of the cosine we found from the triangle in (Figure), and simplify.
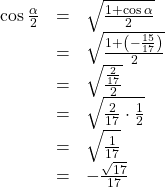
We choose the negative value of
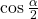 because the angle is in quadrant II because cosine is negative in quadrant II.
because the angle is in quadrant II because cosine is negative in quadrant II. - To find
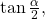 we write the half-angle formula for tangent. Again, we substitute the value of the cosine we found from the triangle in (Figure) and simplify.
we write the half-angle formula for tangent. Again, we substitute the value of the cosine we found from the triangle in (Figure) and simplify.
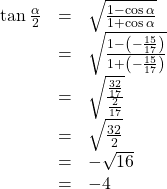
We choose the negative value of
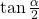 because
because 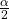 lies in quadrant II, and tangent is negative in quadrant II.
lies in quadrant II, and tangent is negative in quadrant II.
Try It
Given that ![]() and
and ![]() lies in quadrant IV, find the exact value of
lies in quadrant IV, find the exact value of ![]()
Show Solution
![]()
Finding the Measurement of a Half Angle
Now, we will return to the problem posed at the beginning of the section. A bicycle ramp is constructed for high-level competition with an angle of![]() formed by the ramp and the ground. Another ramp is to be constructed half as steep for novice competition. If
formed by the ramp and the ground. Another ramp is to be constructed half as steep for novice competition. If ![]() for higher-level competition, what is the measurement of the angle for novice competition?
for higher-level competition, what is the measurement of the angle for novice competition?
Show Solution
Since the angle for novice competition measures half the steepness of the angle for the high level competition, and ![]() for high competition, we can find
for high competition, we can find ![]() from the right triangle and the Pythagorean theorem so that we can use the half-angle identities. See (Figure 4).
from the right triangle and the Pythagorean theorem so that we can use the half-angle identities. See (Figure 4).

We see that ![]() We can use the half-angle formula for tangent:
We can use the half-angle formula for tangent:![]() Since
Since ![]() is in the first quadrant, so is
is in the first quadrant, so is ![]()

We can take the inverse tangent to find the angle:![]() So the angle of the ramp for novice competition is
So the angle of the ramp for novice competition is ![]()
Access these online resources for additional instruction and practice with double-angle, half-angle, and reduction formulas.
Key Equations
| Double-angle formulas | 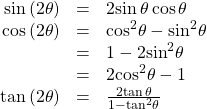 |
| Reduction formulas | 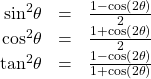 |
| Half-angle formulas | 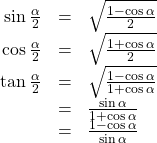 |
Key Concepts
- Double-angle identities are derived from the sum formulas of the fundamental trigonometric functions: sine, cosine, and tangent. See (Figure), (Figure), (Figure), and (Figure).
- Reduction formulas are especially useful in calculus, as they allow us to reduce the power of the trigonometric term. See (Figure) and (Figure).
- Half-angle formulas allow us to find the value of trigonometric functions involving half-angles, whether the original angle is known or not. See (Figure), (Figure), and (Figure).
Section Exercises
Verbal
Explain how to determine the reduction identities from the double-angle identity ![]()
Show Solution
Use the Pythagorean identities and isolate the squared term.
Explain how to determine the double-angle formula for ![]() using the double-angle formulas for
using the double-angle formulas for![]() and
and ![]()
We can determine the half-angle formula for ![]() by dividing the formula for
by dividing the formula for ![]() by
by ![]() Explain how to determine two formulas for
Explain how to determine two formulas for ![]() that do not involve any square roots.
that do not involve any square roots.
Show Solution
![]() multiplying the top and bottom by
multiplying the top and bottom by ![]() and
and ![]() respectively.
respectively.
For the half-angle formula given in the previous exercise for![]() explain why dividing by 0 is not a concern. (Hint: examine the values of
explain why dividing by 0 is not a concern. (Hint: examine the values of ![]() necessary for the denominator to be 0.)
necessary for the denominator to be 0.)
Algebraic
For the following exercises, find the exact values of a) ![]() b)
b) ![]() and c)
and c) ![]() without solving for x.
without solving for x.
If ![]() and
and ![]() is in quadrant I.
is in quadrant I.
Show Solution
a) ![]() b)
b) ![]() c)
c) ![]()
If ![]() and
and ![]() is in quadrant I.
is in quadrant I.
If ![]() and
and ![]() is in quadrant III.
is in quadrant III.
Show Solution
a) ![]() b)
b) ![]() c)
c) ![]()
If ![]() and
and ![]() is in quadrant IV.
is in quadrant IV.
For the following exercises, find the values of the six trigonometric functions if the conditions provided hold.
![]() and
and ![]()
Show Solution
![]()
![]() and
and ![]()
For the following exercises, simplify to one trigonometric expression.
![]()
Show Solution
![]()
![]()
For the following exercises, find the exact value using half-angle formulas.
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
For the following exercises, find the exact values of a) ![]() b)
b) ![]() and c)
and c) ![]() without solving for
without solving for ![]() when
when ![]()
If ![]() and
and ![]() is in quadrant IV.
is in quadrant IV.
If ![]() and
and ![]() is in quadrant III.
is in quadrant III.
Show Solution
a) ![]() b)
b) ![]() c)
c) ![]()
If ![]() and
and ![]() is in quadrant II.
is in quadrant II.
If ![]() and
and ![]() is in quadrant II.
is in quadrant II.
Show Solution
a) ![]() b)
b) ![]() c)
c) ![]()
For the following exercises, use (Figure 5) to find the requested half and double angles.

Find ![]() and
and ![]()
Find ![]() and
and ![]()
Show Solution
![]()
Find ![]() and
and ![]()
Find ![]() and
and ![]()
Show Solution
![]()
For the following exercises, simplify each expression. Do not evaluate.
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
For the following exercises, prove the given identity.
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
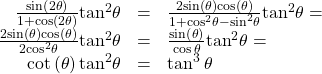
For the following exercises, rewrite the expression with an exponent no higher than 1.
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
Technology
For the following exercises, reduce the equations to powers of one, and then check the answer graphically.
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
![]()
![]()
For the following exercises, algebraically find an equivalent function, only in terms of ![]() and/or
and/or ![]() and then check the answer by graphing both functions.
and then check the answer by graphing both functions.
![]()
Show Solution
![]()
![]()
Extensions
For the following exercises, prove the identities.
![]()
Show Solution
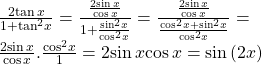
![]()
![]()
Show Solution
![]()
![]()
![]()
Show Solution
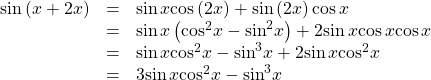
![]()
![]()
Show Solution
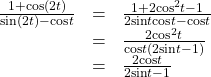
![]()
![]()
Show Solution
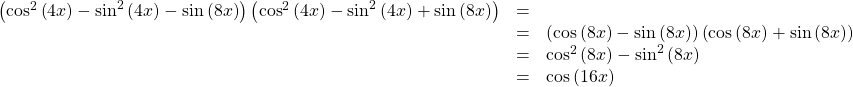
Glossary
- double-angle formulas
- identities derived from the sum formulas for sine, cosine, and tangent in which the angles are equal
- half-angle formulas
- identities derived from the reduction formulas and used to determine half-angle values of trigonometric functions
- reduction formulas
- identities derived from the double-angle formulas and used to reduce the power of a trigonometric function
