Proofs, Identities, and Toolkit Functions
Appendix
Important Proofs and Derivations
Product Rule
![]()
Proof:
Let![]() and
and![]()
Write in exponent form.
![]() and
and![]()
Multiply.
![]()
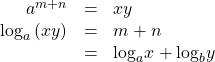
Change of Base Rule
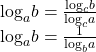
where![]() and
and![]() are positive, and
are positive, and![]()
Proof:
Let![]()
Write in exponent form.
![]()
Take the![]() of both sides.
of both sides.
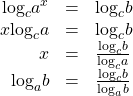
When![]()
![]()
Heron’s Formula
![]()
where![]()
Proof:
Let![]() [latex]b,[/latex]and
[latex]b,[/latex]and![]() be the sides of a triangle, and
be the sides of a triangle, and![]() be the height.
be the height.
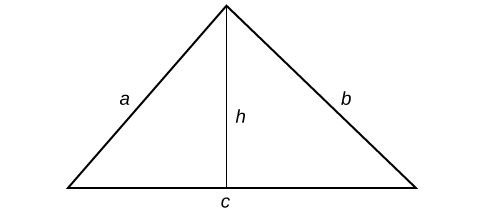
So![]() .
.
We can further name the parts of the base in each triangle established by the height such that![]()
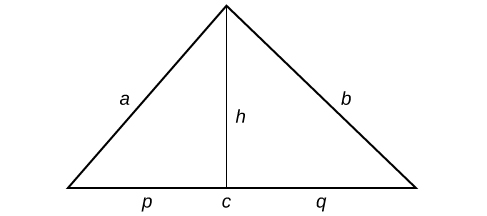
Using the Pythagorean Theorem,![]() and
and![]()
Since![]() then
then![]() Expanding, we find that
Expanding, we find that![]()
We can then add![]() to each side of the equation to get
to each side of the equation to get![]()
Substitute this result into the equation![]() yields
yields![]()
Then replacing![]() with
with![]() gives
gives![]()
Solve for![]() to get
to get
![]()
Since![]() we get an expression in terms of
we get an expression in terms of![]() [latex]b,[/latex]and
[latex]b,[/latex]and ![]()
![Rendered by QuickLaTeX.com \begin{array}{ccc}\hfill {h}^{2}& =& {a}^{2}-{p}^{2}\hfill \\ & =& \left(a+p\right)\left(a-p\right)\hfill \\ & =& \left[a+\frac{\left({a}^{2}+{c}^{2}-{b}^{2}\right)}{2c}\right]\left[a-\frac{\left({a}^{2}+{c}^{2}-{b}^{2}\right)}{2c}\right]\hfill \\ & =& \frac{\left(2ac+{a}^{2}+{c}^{2}-{b}^{2}\right)\left(2ac-{a}^{2}-{c}^{2}+{b}^{2}\right)}{4{c}^{2}}\hfill \\ & =& \frac{\left({\left(a+c\right)}^{2}-{b}^{2}\right)\left({b}^{2}-{\left(a-c\right)}^{2}\right)}{4{c}^{2}}\hfill \\ & =& \frac{\left(a+b+c\right)\left(a+c-b\right)\left(b+a-c\right)\left(b-a+c\right)}{4{c}^{2}}\hfill \\ & =& \frac{\left(a+b+c\right)\left(-a+b+c\right)\left(a-b+c\right)\left(a+b-c\right)}{4{c}^{2}}\hfill \\ & =& \frac{2s\cdot \left(2s-a\right)\cdot \left(2s-b\right)\left(2s-c\right)}{4{c}^{2}}\hfill \end{array}](https://university.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-6ab5f315f65a501ef0426a0f75fe210e_l3.png)
Therefore,
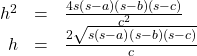
And since![]() then
then
Properties of the Dot Product
![]()
Proof:
![]()
Proof:
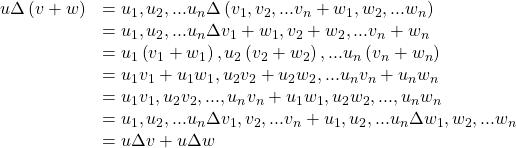
![]()
Proof:
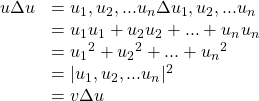
Standard Form of the Ellipse centered at the Origin
![]()
Derivation
An ellipse consists of all the points for which the sum of distances from two foci is constant:
![]()
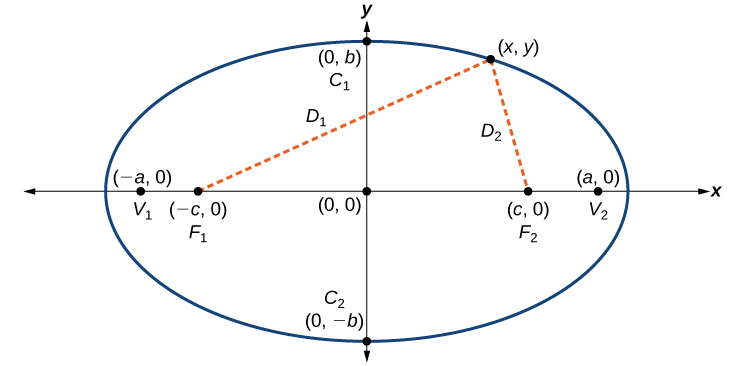
Consider a vertex.
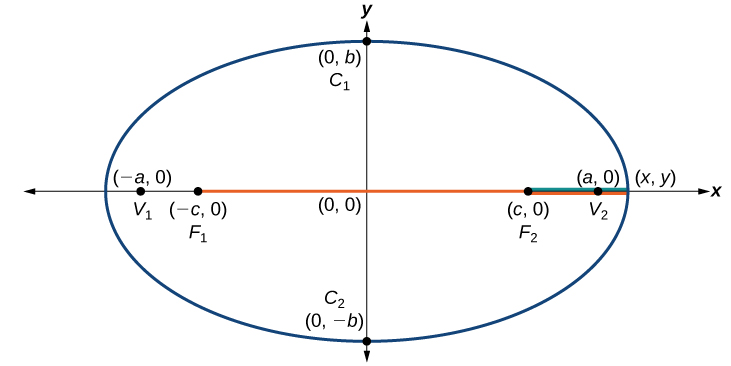
Then,![]()
Consider a covertex.
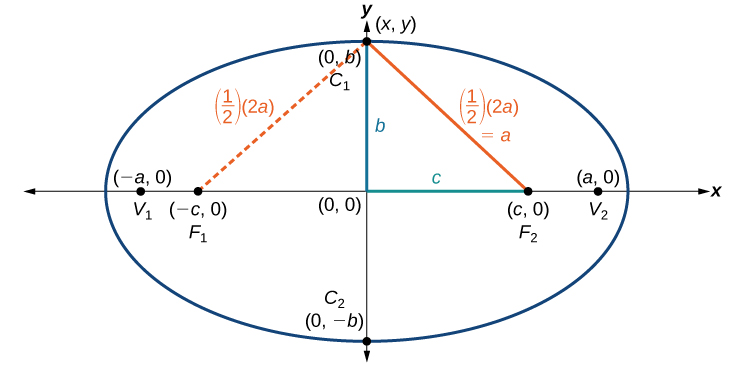
Then![]()
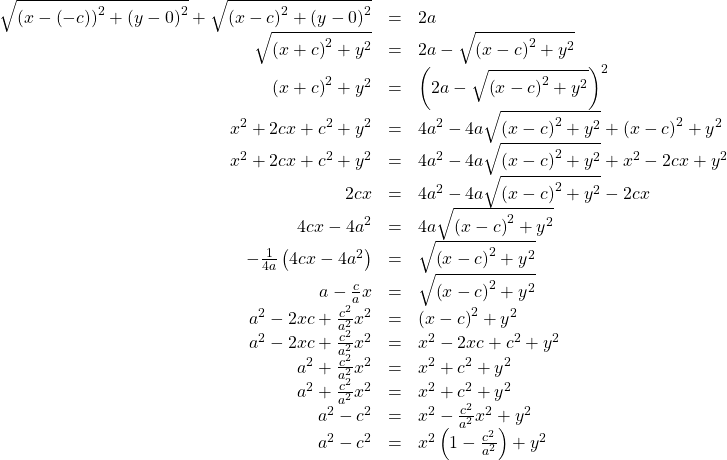
Let![]()
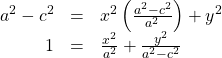
Because![]() then
then![]()
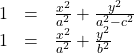
Standard Form of the Hyperbola
![]()
Derivation
A hyperbola is the set of all points in a plane such that the absolute value of the difference of the distances between two fixed points is constant.
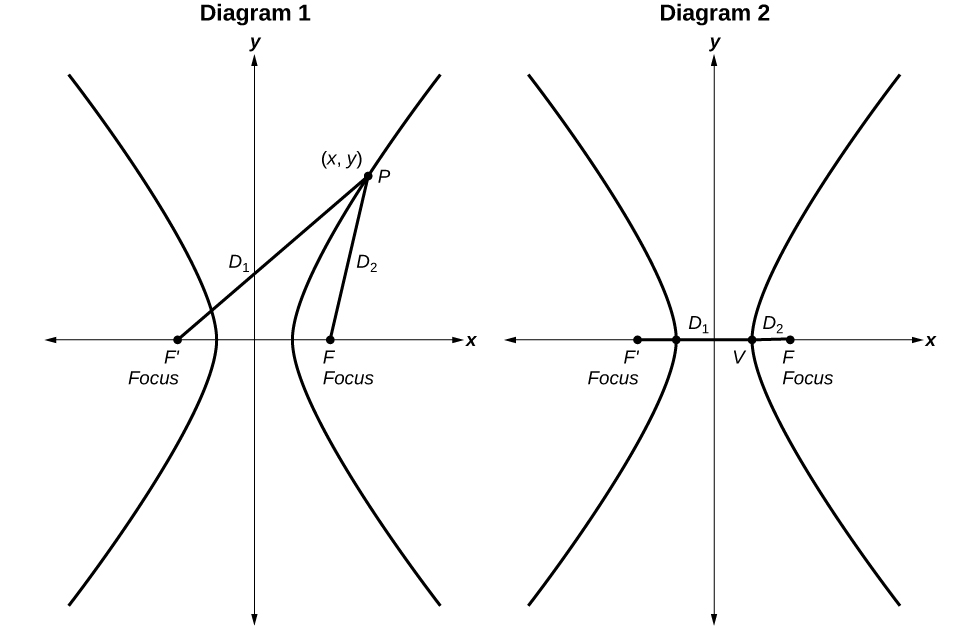
Diagram 1: The difference of the distances from Point P to the foci is constant:
![]()
Diagram 2: When the point is a vertex, the difference is![]()
![]()
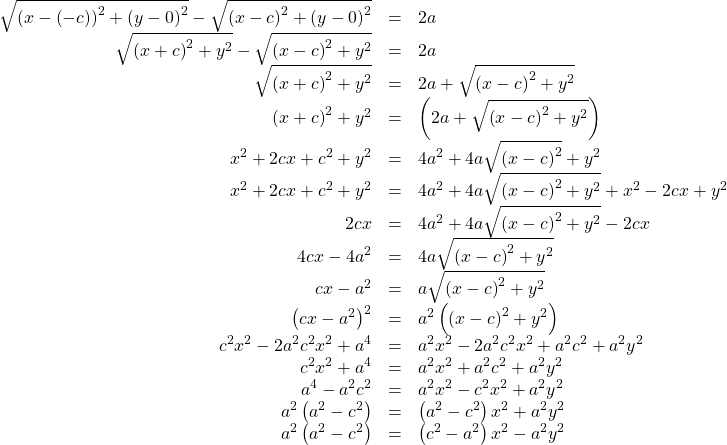
Define![]() as a positive number such that
as a positive number such that![]()
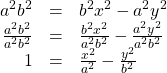
Trigonometric Identities
| Pythagorean Identity | 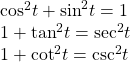 |
| Even-Odd Identities | 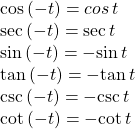 |
| Cofunction Identities | 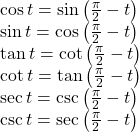 |
| Fundamental Identities | 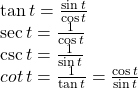 |
| Sum and Difference Identities | 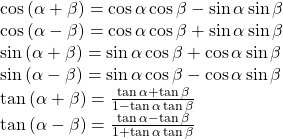 |
| Double-Angle Formulas | 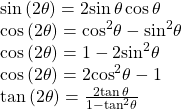 |
| Half-Angle Formulas | 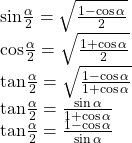 |
| Reduction Formulas | 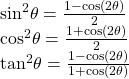 |
| Product-to-Sum Formulas | ![Rendered by QuickLaTeX.com \begin{array}{l}\hfill \\ \mathrm{cos}\alpha \mathrm{cos}\beta =\frac{1}{2}\left[\mathrm{cos}\left(\alpha -\beta \right)+\mathrm{cos}\left(\alpha +\beta \right)\right]\hfill \\ \mathrm{sin}\alpha \mathrm{cos}\beta =\frac{1}{2}\left[\mathrm{sin}\left(\alpha +\beta \right)+\mathrm{sin}\left(\alpha -\beta \right)\right]\hfill \\ \mathrm{sin}\alpha \mathrm{sin}\beta =\frac{1}{2}\left[\mathrm{cos}\left(\alpha -\beta \right)-\mathrm{cos}\left(\alpha +\beta \right)\right]\hfill \\ \mathrm{cos}\alpha \mathrm{sin}\beta =\frac{1}{2}\left[\mathrm{sin}\left(\alpha +\beta \right)-\mathrm{sin}\left(\alpha -\beta \right)\right]\hfill \end{array}](https://university.pressbooks.pub/app/uploads/quicklatex/quicklatex.com-444187d929be8462953f127e5558676e_l3.png) |
| Sum-to-Product Formulas | 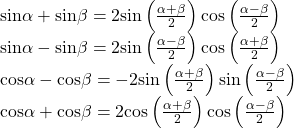 |
| Law of Sines | |
| Law of Cosines | 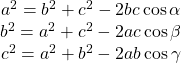 |
ToolKit Functions
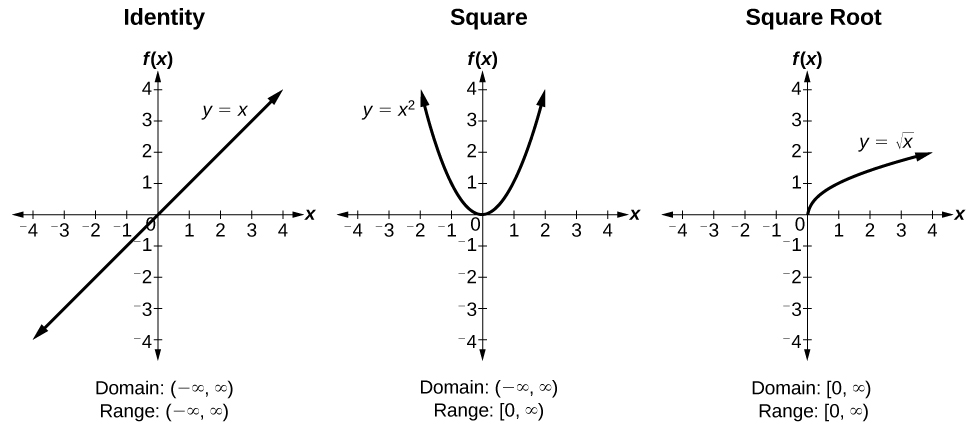
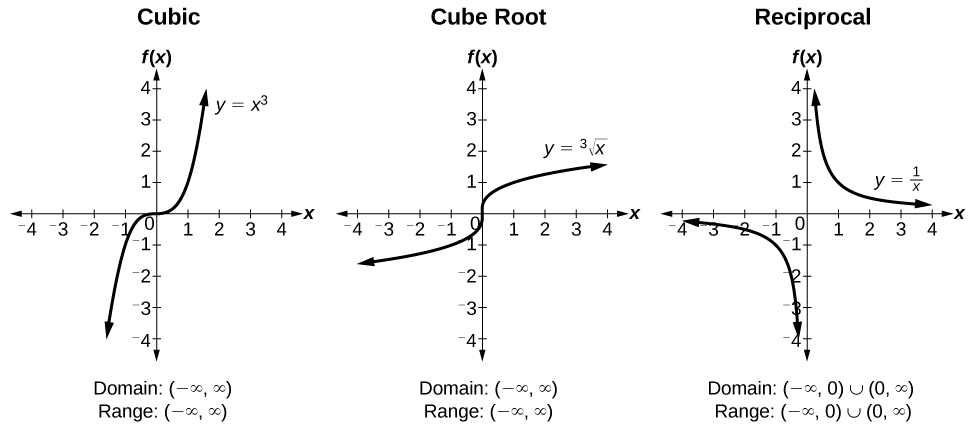
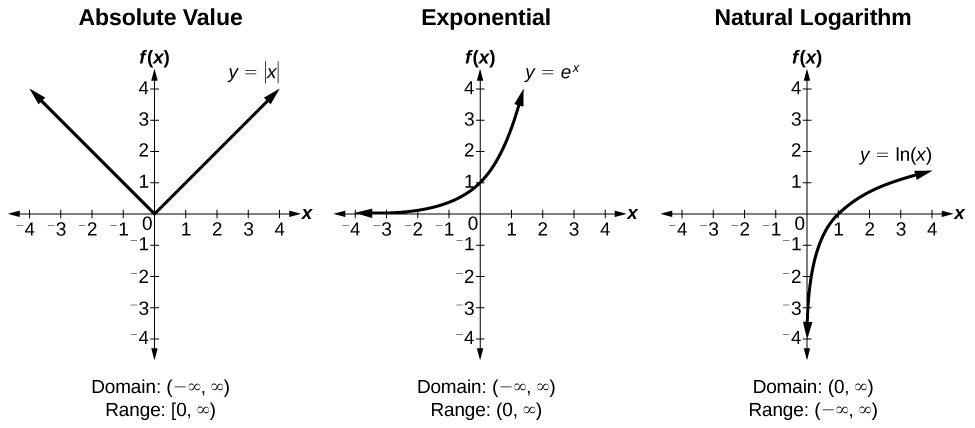
Trigonometric Functions
Unit Circle
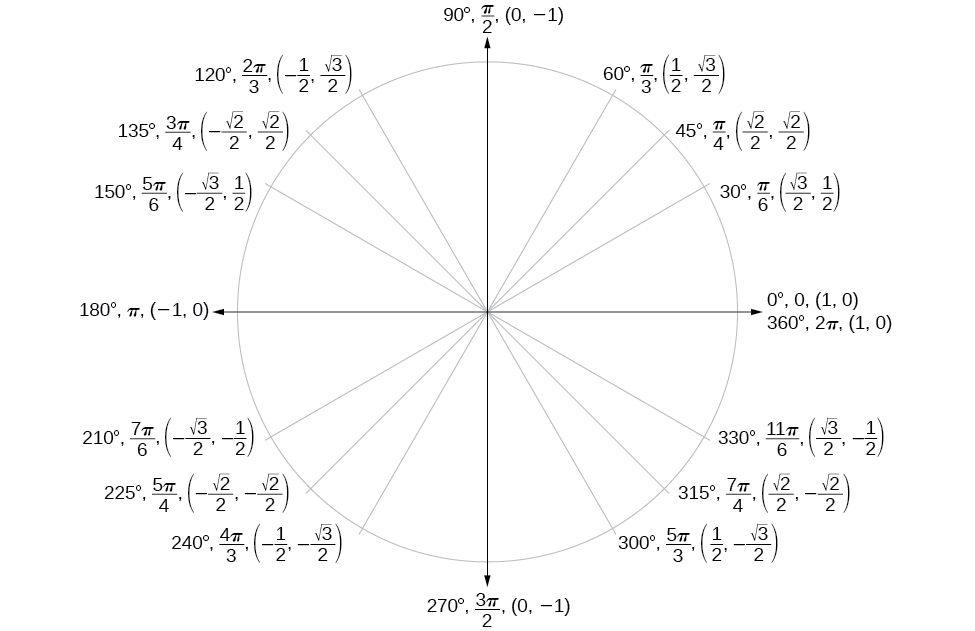
| Angle | |||||
|---|---|---|---|---|---|
| Cosine | 1 | 0 | |||
| Sine | 0 | 1 | |||
| Tangent | 0 | 1 | Undefined | ||
| Secant | 1 | 2 | Undefined | ||
| Cosecant | Undefined | 2 | 1 | ||
| Cotangent | Undefined | 1 | 0 |
